A treliça abaixo representa uma treliça de sustentação do teto de um aeroporto. Em determinado dia um evento cataclísmico rompeu as barras AB, CD, EF e GH da treliça. Determine:

- O tipo de estrutura antes do rompimento (treliçada ou não)
- O tipo de estrutura após o rompimento (treliçada ou não)
Passo 1
Antes de tudo precisamos analisar o seguinte. As perguntas principais se focam em definir se a estrutura é ou não treliçada. Para definirmos se uma estrutura é treliçada precisamos fazer a analise de nós. Após a analise de nós também precisamos verificar o número de diagonais por polígono da nossa estrutura, sabemos que
Se o número de diagonais por polígono quadrangular for maior que uma diagonal, nossa estrutura será hiperestática internamente, e nesse caso, podemos romper uma dessas diagonais excedentes que ainda teremos uma estrutura isostática, dito isso, vamos por a mão na massa

Passo 2
Analisando primeiro a estrutura antes do rompimento, conseguimos ver que temos polígonos com duas diagonais, o que já caracteriza a nossa treliça como hiperestática internamente, e podemos ver aqui 3 casos de hiperestaticidade interna como marcado na figura abaixo
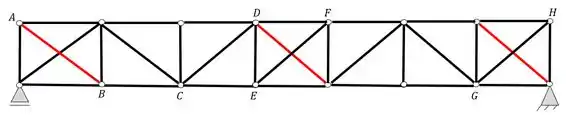
Agora precisamos ver se podemos caracteriza-la como treliça, para isso basta fazermos a regra do triângulo na nossa estrutura e ver se bate, já sabemos que o primeiro passo sempre é escolher dois nós consecutivos e a partir deles dois chegar em todos os outros através de triângulos, fazendo isso na nossa estrutura teremos

Mas perceba que interessante, nos casos que avaliamos os nós com duas diagonais podemos determinar o ponto 4 de duas formas, uma usando o nó 2 e 3

Ou podemos usar o nós 1 e 2 também
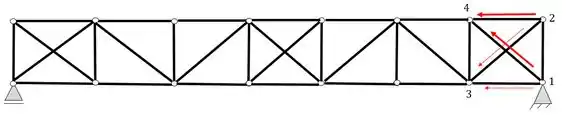
Por isso caracterizamos a nossa estrutura como hiperestática internamente, agora só, continuarmos o processo até chegarmos no último nó.
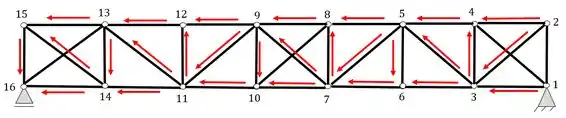
Podemos ver que de fato conseguimos chegar no ultimo nó, logo, de fato, a nossa estrutura antes do rompimento é treliçada (já que respeita a regra dos triângulos) e de fato, pelos apoios dela, é uma estrutura isostática devido aos apoios, vamos agora analisar a nossa estrutura após o rompimento das barras.
Passo 3
A primeira coisa que faremos é arrancar todas as barras que romperam e fazer exatamente o que fizemos no passo anterior, mas agora sem as barras rompidas, com isso teremos primeiro a seguinte estrutura

Precisamos agora definir dois nós iniciais consecutivos, e agora irei definir esses dois nós começando pelo lado esquerdo da treliça, e a partir deles definiremos os próximos nós com isso temos

A partir do nó 3 definimos o próximo nó, que é o 4

A partir do nó 4 definimos o próximo nó, que é o 5, e a partir do 5 definiremos o 6


Agora perceba o seguinte, a partir dos nós 5 e 6 é impossível definir o nó 7 através de um triangulo, ou seja, a estrutura não é treliçada, pelos apoios é uma estrutura do tipo isostática, e ainda vemos que os polígonos apresentam apenas uma diagonal, sendo assim, não é mais uma estrutura do tipo hiperestática internamente.
Resposta
- É uma estrutura do tipo treliçada
- Não é uma estrutura do tipo treliçada