Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Condições de Contorno

Ver Teoria
Exercício 41235678

Enunciado

(Adaptada) Um líquido escoa para baixo sobre uma superfície plana inclinada em um filme laminar, permanente, completamente desenvolvido e de espessura h . Considerando as equações da continuidade e Navier-Stokes simplificadas abaixo, obtenha expressões para o perfil de velocidades do líquido, a distribuição de tensões de cisalhamento, a vazão volumétrica e velocidade média. Relacione a espessura do filme de líquido com a vazão volumétrica por unidade de água com espessura h   =   1   m m , escoando sobre uma superfície de largura b   =   1   m , inclinada de θ = 15 ° em relação à horizontal.

Equação da continuidade simplificada

∂ v ∂ y = 0

Equação de Navier-Stokes simplificada

0 =   ρ g x + μ ∂ 2 u ∂ y 2

0 =   ρ g y + ∂ p ∂ y

Passo 1

UAU! Esse exercício pediu coisa para caramba, mas nem deu tanta informação assim! Quem poderá nos defender?

Primeiro, vamos ilustrar o que está acontecendo:

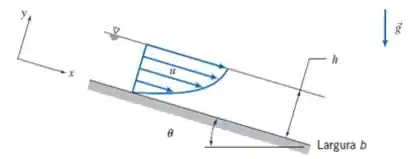
Temos duas condições de contorno. Uma delas é a condição de não deslizamento. Na placa, ou seja em y = 0, a velocidade u do fluido é 0, pois a placa está parada.

u   =   0   e m   y   =   0

A outra está relacionada a superfície livre, ou seja, na superfície do fluido mais distante da placa (y=h). Já que não há um sólido ali para que seja possível aplicar uma força paralela ao movimento, podemos considerar que a tensão de cisalhamento ali é zero!

τ x y y = h =   0

Lembrando que a água é um fluido newtoniano, vale a Lei de Newton da Viscosidade

τ x y =   μ d u d y

Logo, a taxa de deformação du/dy será zero em y = h

d u d y y = h = 0

Essas são as condições de contorno que vão nos ajudar a resolver a questão. Vamos voltar para as equações então?

Passo 2

As equações de Navier-Stokes simplificadas para esse caso foram dadas no enunciado e são essas aqui:

0 =   ρ g x + μ ∂ 2 u ∂ y 2

0 =   ρ g y + ∂ p ∂ y

Para descobrir o perfil de velocidade que o enunciado pediu, vamos integrar a primeira equação, beleza? Vamos isolar o termo no qual a velocidade u aparece!

0 =   ρ g x + μ ∂ 2 u ∂ y 2   ⇒   d 2 u d y 2 = - ρ g x μ

Daí, pela geometria do problema, a componente da gravidade na direção x é:

g x = g   s e n   θ

Substituindo em Navier-Stokes

d 2 u d y 2 = - ρ g s e n   θ μ

Agora sim, hora de integrar. No lado direito, nenhuma variável depende de y 😉

d u d y = - ρ g s e n   θ μ y +   c 1

Precisamos integrar mais uma vez

u = - ρ g s e n   θ μ y 2 2 + c 1 y + c 2

Passo 3

Para descobrir c 1 e c 2 , vamos aplicar as condições do contorno no Passo 1. A primeira foi a condição de não deslizamento:

u   =   0   e m   y   =   0

Aplicando no perfil de velocidade

0 = - ρ g s e n   θ μ 0 2 2 + c 1 0 + c 2

c 2 = 0

Atualizando o perfil de velocidade:

u = - ρ g s e n   θ μ y 2 2 + c 1 y

A segunda condição de contorno foi da tensão cisalhante na superfície livre (y=h)

d u d y y = h = 0

A expressão de du/dy é

d u d y = - ρ g s e n   θ μ y +   c 1

Em y=h:

d u d y y = h = - ρ g s e n   θ μ h +   c 1

0 = - ρ g s e n   θ μ h +   c 1

Logo

c 1 = ρ g h s e n   θ μ

Atualizando o perfil de velocidades

u = - ρ g s e n   θ μ y 2 2 + ρ g h s e n   θ μ y

Colocando em evidência

u = ρ g s e n   θ μ h y - y 2 2

Show! Encontramos o perfil de velocidades usando as condições de contorno! Com ele dá para achar a expressão da tensão cisalhante

Passo 4

Para achar a distribuição de tensão de cisalhamento, vamos usar a Lei de Newton da Viscosidade

τ x y =   μ d u d y

No passo anterior descobrimos u, logo du/dy é:

d u d y = ρ g s e n   θ μ h - y

Substituindo na Lei de Newton da Viscosidade:

τ x y =   μ ρ g s e n   θ μ h - y

τ x y =   ρ g s e n   θ   h - y

E essa é a distribuição de tensão cisalhante

Passo 5

Agora é a vez da vazão volumétrica. Vamos usar a definição de vazão:

Q =   ∫ A u d A

A área é a área transversal do escoamento. É uma largura b (entrando na tela) multiplicada pela altura y

Q =   ∫ 0 h u b d y

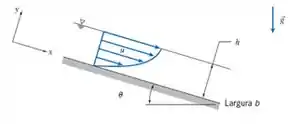
Sabemos que u é o perfil de velocidade

Q =   ∫ 0 h ρ g s e n   θ μ h y - y 2 2 b d y

Integrando

Q =   ρ g b   s e n   θ μ h 3 2 - h 3 6

Q =   ρ g b   s e n   θ μ h 3 3

Essa é a vazão volumétrica :D Suuucesso! Agora, vamos calcular a velocidade média.

Passo 6

Sei que é muita coisa, mas a velocidade média já tá quase toda calculada. Ela é vazão volumétrica sobre área transversal

V - =   Q A

Acabamos de calcular Q, vamos substituir

V - =   ρ g b   s e n   θ μ h 3 3 b h

Simplificando

V - =   ρ g   s e n   θ μ h 2 3

Viu! Rapidinho achamos :D

Passo 7

Finalmente, vamos lembrar da última parte do enunciado

“Relacione a espessura do filme de líquido com a vazão volumétrica em um filme de água com espessura h   =   1   m m , escoando sobre uma superfície de largura b   =   1   m , inclinada de θ = 15 ° em relação à horizontal.”

Traduzindo: encontre a vazão volumétrica utilizando esses números indicados na figura

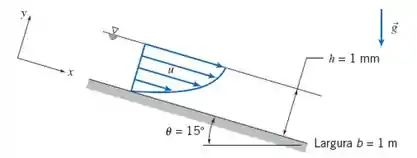
Lembrando que já calculamos a expressão da vazão volumétrica

Q =   ρ g b   s e n   θ μ h 3 3

Substituindo b = 1   m ,     h   =   1   m m = 0,001   m ,   θ = 15 °

Q =   ρ g . 1 .   s e n   15 ° μ 0,001 3 3

Como o fluido é a água

Q =   1000.9,8.1 .   s e n   15 ° 0,001 0,001 3 3

Q = 8,5 . 10 - 4   m 3 / s

Q = 0,85   L / s

YAY! Fechamos o exercício 😉 Foi longo, mas olha quanta coisa conseguimos achar utilizando as condições de contorno em Navier-Stokes!

Resposta

Perfil de velocidade

u = ρ g s e n   θ μ h y - y 2 2

Distribuição de tensões de cisalhamento

τ x y =   ρ g s e n   θ   h - y

Expressão de vazão volumétrica

Q =   ρ g b   s e n   θ μ h 3 3

Velocidade média

V - =   ρ g   s e n   θ μ h 2 3

Vazão volumétrica para b = 1   m ,     h   =   1   m m = 0,001   m ,   θ = 15 °

Q = 0,85   L / s

Exercícios de Livros Relacionados

O método euleriano de análise do escoamento de fluidos é mais semelhante ao estudo de um sistema ou de um volume de controle? Explique.
Aproximamos o escoamento do ar em um acessório de aspirador de pó seguindo as componentes da velocidade no plano central (o plano x y ): u = - V ˙ x π L x 2 + y 2 + b 2 x 4 + 2 x 2 y 2 + 2 x 2 b 2 + y
Considerando a metade a montante x0 doo campo de escoamento do Problema 4-94 (escoamento sobre um cilindro circular) . Introduzindo um parâmetro chamado função de corrente ψ , que é constante ao longo
Considere um campo de escoamento em regime permanente e bidimensional cuja componente x da velocidade é dada por u = a + b x - c 2 Onde a ,b e c são constante com dimensões apropriadas. Com qual forma
Considere o campo de escoamento do Problema 4-94 (escoamento sobre um cilindro circular). Calcule as duas taxas de deformação linear no plano r θ ; ou seja, calcule ε r r e ε θ θ . Discuta se os segme