Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Condições de Contorno

Ver Teoria
Exercício 81234567

Enunciado

Um filme de espessura constante de um líquido viscoso flui em movimento laminar descendo por uma placa inclinada a um ângulo θ , como na Figura. O perfil de velocidade é:

u = C y 2 h - y                               v = w = 0

Encontre a constante C   em termos do peso específico e da viscosidade e do ângulo θ . Encontre a vazão volumétrica Q por unidade de largura em termos desses parâmetros.

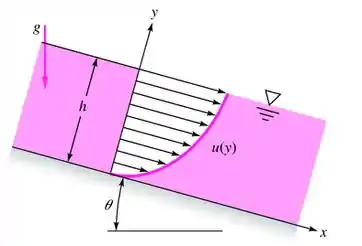
Passo 1

Fala galera! Então esse exercício envolve um pouquinho de Equação da Continuidade, um pouco de Navier-Stokes e no final vamos aplicar as condições de contorno que o problema nos fornece.

Temos as seguintes informações de contorno:

p x , y = h = p a

u y = 0 = 0

Líquidos são normalmente incompressíveis e apresentam viscosidade constante:

ρ = c o n s t a n t e

μ = c o n s t a n t e

Passo 2

Vamos checar para ver se a continuidade é satisfeita nesse escoamento:

∂ ρ ∂ t + ∂ ∂ x ρ u + ∂ ∂ y ρ v + ∂ ∂ z ρ w = 0

Aplicando nosso campo de velocidades:

u = C y 2 h - y ,   v = w = 0

Sobra o seguinte termo

∂ ∂ x ρ u = 0

Que também é zero, logo o escoamento satisfaz a continuidade.

Passo 3

Como a massa específica e a viscosidade são constantes, podemos utilizar as esquações de Navier-Stokes:

ρ g x - ∂ p ∂ x + μ ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 + ∂ 2 u ∂ z 2 = ρ ∂ u ∂ t + u ∂ u ∂ x + v ∂ u ∂ y + w ∂ u ∂ z

ρ g y - ∂ p ∂ y + μ ∂ 2 v ∂ x 2 + ∂ 2 v ∂ y 2 + ∂ 2 v ∂ z 2 = ρ ∂ v ∂ t + u ∂ v ∂ x + v ∂ v ∂ y + w ∂ v ∂ z

Sabemos que u depende apenas de y e que v = w = 0

ρ g x - ∂ p ∂ x + μ ∂ 2 u ∂ y 2 = 0

ρ g y - ∂ p ∂ y = 0

Se decompormos a força gravitacional g nas componentes x , y fornecidadas:

g x = g sin ⁡ θ

g y = g cos ⁡ θ

Substituindo na primeira expressão o valor de u = C y 2 h - y e g x :

ρ g sin ⁡ θ - ∂ p ∂ x + μ - 2 C = 0

- 2 μ C = ∂ p ∂ x - ρ g sin ⁡ θ

Se p x , h = p a , em qualquer x a pressão é constante. Logo:

2 μ C = ρ g sin ⁡ θ

C = ρ g sin ⁡ θ 2 μ

Ou em função do peso específico γ = ρ g

C = γ sin ⁡ θ 2 μ

Passo 4

Sabemos de quando calculávamos vazão que:

Q = ∫ V d A

No nosso caso calcularemos a vazão por unidade de largura, que no caso é z

Se d A = d y d z

Q = ∫ 0 h u   d y = ∫ 0 h C y 2 h - y   d y

Q = ∫ 0 h 2 C h y - C y ²   d y

Q = C h y ² - C 3 y ³ h 0

Q = 2 3 C h 3

Substituindo C = γ sin ⁡ θ 2 μ

Q = 1 3 h 3 γ sin ⁡ θ μ

Resposta

Letra a)

C = γ sin ⁡ θ 2 μ

Letra b)

Q = 1 3 h 3 γ sin ⁡ θ μ

Exercícios de Livros Relacionados

O método euleriano de análise do escoamento de fluidos é mais semelhante ao estudo de um sistema ou de um volume de controle? Explique.
Aproximamos o escoamento do ar em um acessório de aspirador de pó seguindo as componentes da velocidade no plano central (o plano x y ): u = - V ˙ x π L x 2 + y 2 + b 2 x 4 + 2 x 2 y 2 + 2 x 2 b 2 + y
Considerando a metade a montante x0 doo campo de escoamento do Problema 4-94 (escoamento sobre um cilindro circular) . Introduzindo um parâmetro chamado função de corrente ψ , que é constante ao longo
Considere um campo de escoamento em regime permanente e bidimensional cuja componente x da velocidade é dada por u = a + b x - c 2 Onde a ,b e c são constante com dimensões apropriadas. Com qual forma
Considere o campo de escoamento do Problema 4-94 (escoamento sobre um cilindro circular). Calcule as duas taxas de deformação linear no plano r θ ; ou seja, calcule ε r r e ε θ θ . Discuta se os segme