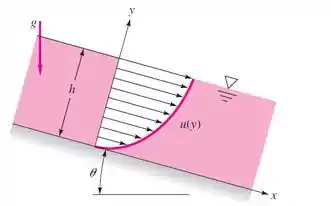
Para o filme líquido (viscoso) de espessura constante sendo drenado na figura a seguir, quais são as condições de contorno apropriadas (a) no fundo em y = 0 e (b) na superfície em y = h?
Passo 1
Esse exercício nos pede as condições de contorno. Analisando o fundo desse escoamento, ou seja, onde y = 0, temos uma parede, certo?
Isso significa que temos uma condição de fronteira. Assim, podemos aplicar em , a condição de não deslizamento, ou a hipótese de não-escorregamento
Nesse exercício, a velocidade é , logo
Como a parede está parada (no enunciado não há nada informando se a superfície está em movimento), então a velocidade do fluido naquele ponto será zero
Então, a condição de contorno no fundo é
Passo 2
Agora vamos analisar a superfície superior do escoamento, ou seja, onde y = h
Nessa parte não há uma parede. Então não podemos aplicar a condição de não deslizamento. Porém, se não há parede (placa ou barreira), não há tensão cisalhante
Considerando que o fluido é newtoniano, ele obedece a Lei de Newton da Viscosidade
A tensão cisalhante é 0 em y = h, logo
No fluido newtoniano, a viscosidade é constante, então:
E essa é a condição de contorno na superfície em y = h.
Resposta
a)
b)