Exercícios Resolvidos de Condições de Contorno

Ver Teoria

Exercício 1 2 3 4 5 6 7 8

Enunciado

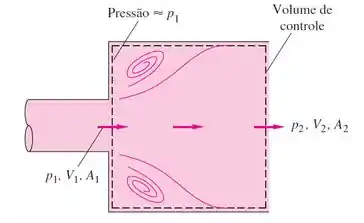
Vamos analisar a expansão brusca do escoamento no tubo da figura, usando as equações completas da continuidade e de Navier-Stokes. Quais são as condições de contorno apropriadas para lidar com esse problema?

Obs: Quando o escoamento em um tubo se alarga bruscamente, como na figura, aparecem turbilhões de baixa velocidade e baixo atrito nos cantos, e o escoamento gradualmente se alarga até A2 a jusante.

Passo 1

Opa! Para encontrar as condições de contorno, vamos por partes. Nesse exercício, temos:

- condições de fronteira (paredes)

- condições de entrada/saída (velocidade)

- condições de entrada/saída (pressão)

Com essas condições, conseguimos utilizar e simplificar as equações da continuidade e Navier-Stokes.

Como são tubos, vamos adotar a coordenada r para o raio e z para a direção do escoamento, ok? Então vamos lá, começando pelas condições de fronteira.

Todas as paredes são fronteiras. E como o enunciado não menciona que esse tubo está em movimento, então vamos considerar que ele está parado (velocidade = 0).

Logo, pela condição de não-escorregamento, a velocidade do fluido nas paredes é zero

As paredes correspondem a , , além da superfície vertical onde ocorre o aumento brusco de raio. Logo, as velocidades e nesses pontos são nulas

Essas são as condições de contorno de fronteira

Passo 2

Para as condições de contorno de entrada (1), devemos considerar que a distribuição de velocidades é conhecida na primeira parte da tubulação a partir de um certo

Além disso, na saída (2) precisamos conhecer também o comportamento da velocidade. Isso acontece a partir de , após os turbilhões de velocidade se estabilizarem.

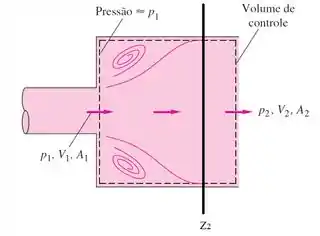
Finalmente, precisamos definir como condição de contorno a entrada ou a saída da pressão. Assim, utilizando a equação da Continuidade e Navier-Stokes será possível calcular a pressão na seção que se deseja conhecer (saída ou entrada)

Em geral, conhecemos a entrada dos escoamentos e queremos saber o que acontece na saída. Fazendo a hipótese de que a pressão na entrada (1) é conhecida, temos a seguinte condição válida:

E assim encontramos todas as condições de contorno para aplicar a continuidade e Navier-Stokes nesse problema. 😊

Resposta

Condições de fronteira (parede):

Condições de entrada/saída:

Exercícios de Livros Relacionados

O método euleriano de análise do escoamento de fluidos é mais semelhante ao estudo de um sistema ou de um volume de controle? Explique.

Aproximamos o escoamento do ar em um acessório de aspirador de pó seguindo as componentes da velocidade no plano central (o plano x y ): u = - V ˙ x π L x 2 + y 2 + b 2 x 4 + 2 x 2 y 2 + 2 x 2 b 2 + y

Considerando a metade a montante x0 doo campo de escoamento do Problema 4-94 (escoamento sobre um cilindro circular) . Introduzindo um parâmetro chamado função de corrente ψ , que é constante ao longo

Considere um campo de escoamento em regime permanente e bidimensional cuja componente x da velocidade é dada por u = a + b x - c 2 Onde a ,b e c são constante com dimensões apropriadas. Com qual forma

Considere o campo de escoamento do Problema 4-94 (escoamento sobre um cilindro circular). Calcule as duas taxas de deformação linear no plano r θ ; ou seja, calcule ε r r e ε θ θ . Discuta se os segme