(Adaptada) Propõe-se para o resfriamento do ar de um cilindro de câmara de combustão a colocação de um conjunto de aletas anulares () na parede do cilindro ().
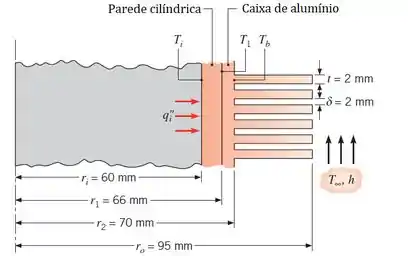
O ar está a e o coeficiente de convecção correspondente é . Mesmo o aquecimento da superfície interna sendo periódico, é razoável considerar condições de regime estacionário com um fluxo de calor médio de .
Considerando desprezível a residência de contato entre a parede e a aleta, determine a temperatura interna da parede ().
Passo 1
Podemos representar a situação com o seguinte esquema:
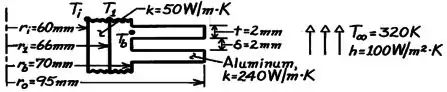
O circuito que representa o sistema é ilustrado abaixo:
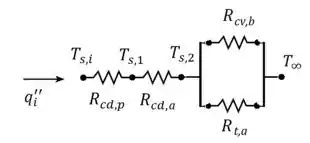
Em que:
Passo 2
A gente pode, então, escrever a taxa de calor em termos das resistências:
Bora calcular as resistências! Começando pela condução na parede:
Para a condução na base da aleta:
Para a convecção na base da aleta:
Como a espessura da aleta () e o espaçamento entre elas () são iguais, a gente pode considerar que a área da base () é metade de toda a área cilíndrica (se não tivesse aletas) e metade é ocupada por aletas. Sendo assim:
Passo 3
Agora, bora calcular a resistência térmica do sistema aletado:
Temos que determinar a eficiência da aleta (). Para isso, vamos utilizar o gráfico desse tipo de geometria:
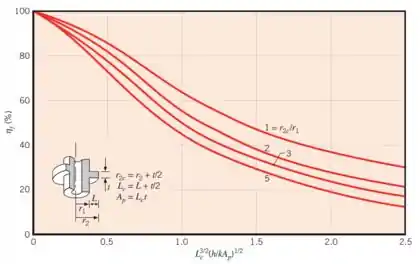
Precisamos, então, saber qual das quatro curvas representa nosso problema e qual o valor de do gráfico. Então, bora lá:
Passo 4
Agora, vamos à resistência que mais interessa:
- Resistência térmica de uma aleta anular simples:
Da expressão aqui em cima, a gente só sabe o coeficiente , mas precisamos determinar a área () e eficiência da aleta ().
A área da aleta é essa área aqui em vermelho:
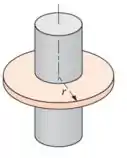
Então, a gente pode escrever que:
Mas a gente pode usar aquela estratégia do raio corrigido (), que é quando a gente assume que a contribuição da área lateral é adicionada à área do disco. Sendo assim:
Em que:
Substituindo os valores do enunciado:
Passo 5
Agora só falta a eficiência ()! Pra calcular a eficiência desse formato de aleta (anular), a gente tem que utilizar o gráfico que já vimos:
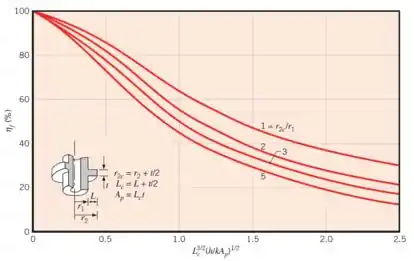
Para determinar a eficiência, a gente precisa então saber qual das quatro curvas representa a nossa aleta e calcular com o valor desse eixo aí loucão. Então, bora lá!
Bora calcular o valor de x do gráfico:
Em que e são calculados pelas expressões mostradas no gráfico:
Além disso:
Ufa! Agora a gente pode finalmente calcular o valor de x:
Pra saber qual das curvas serve pra gente, precisamos calcular a razão entre os raios:
Não tem nenhuma curva com esse valor, mas a gente pode colocar mais ou menos entre as curvas de razão igual a e , um pouco mais próximo da curva de .
Agora a gente já pode marcar no gráfico a posição da abscissa e ver a eficiência correspondente:
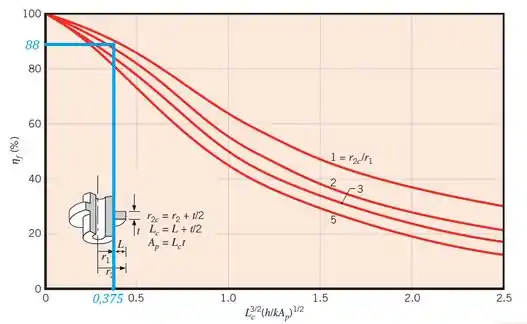
Concluimos, assim, que:
Passo 6
Com a área e eficiência calculadas, a gente pode finalmente determinar a resistência térmica da aleta:
Logo:
Passo 7
Como a gente viu, a taxa de calor por ser escrita como:
E a taxa pode ser escrita em termos do fluxo:
Dividindo a expressão pelo comprimento:
Isolando a temperatura da superfície mais interna (), a gente fica com: