Passagens alteradas são formadas frequentemente entre placas paralelas para elevar a transferência de calor por convecção em matrizes compostas de trocadores de calor. Uma aplicação importante encontra-se em resfriamento de equipamentos eletrônicos, em que um ou mais canais de ar resfriado são colocados entre componentes elétricos que dissipam calor. Considere um canal simples de aletas retangulares de comprimento e espessura , com condições de convecção correspondentes a e .
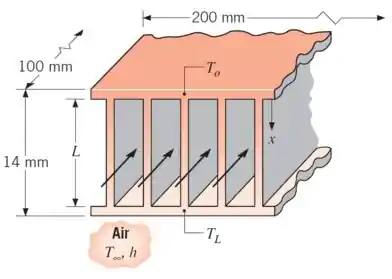
Obtenha expressões para as taxas de transferência de calor da aleta ( e ) em função das temperaturas da base (e ).
Em uma aplicação específica, um canal com de largura e de profundidade contém aletas, casa uma com comprimento . O canal é feito em alumínio () com de espessura ao longo de sua extensão. Se as limitações de temperaturas associadas com os componentes elétricos fixados no lado oposto da placa estabelecem a máxima temperatura permitida na placa e , quais são as potências dissipadas correspondentes de e ?
Passo 1
Obtenha expressões para as taxas de transferência de calor da aleta ( e ) em função das temperaturas da base (e ).
A solução geral para a distribuição de temperatura é dada por:
A gente pode propor as seguintes condições de contorno:
Substituindo na equação:
Dessa maneira:
E, substituindo essa expressão de na equação, a gente consegue achar ainda a constante :
Finalmente, temos que o perfil de temperatura é dado por:
Reorganizando:
Ou, em termos de funções trigonométricas hiperbólicas:
Passo 2
Para encontrar a taxa de calor da aleta, vamos usar a equação de Fourier:
Então, a gente precisa da derivada do perfil de temperatura. Bora calcular então:
A área pode ser calculada como:
Substituindo essas expressões na equação de Fourier:
Na posição , temos:
Na posição , temos:
Passo 3
Em uma aplicação específica, um canal com de largura e de profundidade contém aletas, casa uma com comprimento . O canal é feito em alumínio () com de espessura ao longo de sua extensão. Se as limitações de temperaturas associadas com os componentes elétricos fixados no lado oposto da placa estabelecem a máxima temperatura permitida na placa e , quais são as potências dissipadas correspondentes de e ?
Para calcular as taxas, a gente precisa determinar o valor de , então bora lá:
Substituindo os valores
Assim, o produto vale:
Dessa maneira, na posição , temos:
Dessa maneira, na posição , temos:
Resposta