Como mais e mais componentes são colocados em um circuito integrado individual (chip), a quantidade de calor que é disputado tende a aumentar. Por outro lado, esse aumento está limitado pela temperatura máxima permitida de operação do chip, que é aproximadamente . Para maximizar a dissipação de calor, propõe-se utilizar uma matrix de aletas de cobre () em forma de pino que podem ser fixadas através de processos metalúrgicos a superfície externa de um chip quadrado de de lado.
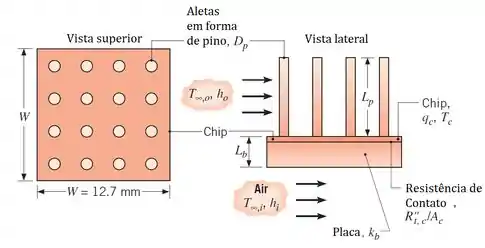
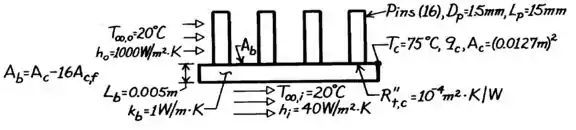
Condições: , , , e .
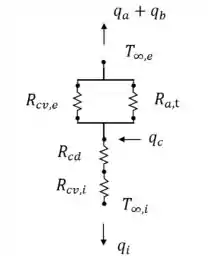
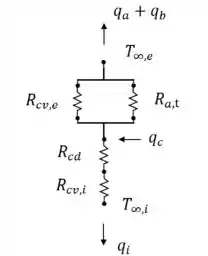
Esboce o circuito térmico equivalente para a montagem pino-placa, considerando condições de estado estacionário unidimensional e resistência de contato desprezível entro os pinos e o chip. Na forma de variáveis, enumere as resistências apropriadas, temperaturas e taxas de calor.
Para as condições prescritas anteriormente, qual é a máxima taxa na qual o calor pode ser dissipado no chip quando os pinos estão no lugar? Isto é, qual é o valor de para ? O diâmetro e o comprimento do pino são respectivamente e .
Passo 1
Esboce o circuito térmico equivalente para a montagem pino-placa, considerando condições de estado estacionário unidimensional e resistência de contato desprezível entro os pinos e o chip. Na forma de variáveis, enumere as resistências apropriadas, temperaturas e taxas de calor.
A situação pode ser ilustrada com esse esquema aqui embaixo:
A gente sabe, pelo enunciado, que o calor que e gerado no chip será dissipado, tanto para a região externa quanto para a região interna.
Nesse caso, temos aletas perdendo calor para o ambiente externo, além da área da base que também perde calor por convecção. Diante disso, é como se houvesse dois mecanismos em paralelo e o circuito pode ser representado da seguinte forma:
Em que:
Passo 2
Para as condições prescritas anteriormente, qual é a máxima taxa na qual o calor pode ser dissipado no chip quando os pinos estão no lugar? Isto é, qual é o valor de para ? O diâmetro e o comprimento do pino são respectivamente e .
Fazendo um balanço de energia na superfície do chip, a gente pode escrever que:
Em que:
- é a taxa de calor proveniente o chip.
- é a taxa de calor dissipada pelo conjunto de aletas.
- é a taxa de calor dissipada pela base do sistema para o ambiente externo.
- é a taxa de calor dissipada para o ambiente interno.
Passo 3
Bora agora calcular cada uma dessas taxas. Começando pela taxa de calor , podemos expressá-la em termos das resistências:
Calculando as resistências...
Para a resistência de convecção interna:
Dessa maneira, temos que:
Passo 4
Bora calcular agora a taxa de calor dissipada pela base da aleta ()!
Como é uma taxa de convecção, temos que:
A área de troca térmica será toda essa região em vermelho/rosa mais escuro, pois é a região que não foi ocupada por aletas:
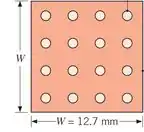
Então, a gente fica com:
Sendo assim:
Passo 5
Agora, finalmente, bora calcular a taxa de calor dissipada pelo conjunto de aletas ().
Em termos da resistência do sistema aletado:
Dessa equação, a gente só precisa determinar a eficiência da aleta () – via gráfico - e calcular a área total ()!
Ou a gente pode usar direto a equação da taxa que temos na tabela. Como essa situação se enquadra no caso (convecção na extremidade), a expressão da taxa é dada por:
O número multiplicando a expressão representa o número de aletas no sistema e:
Sendo assim:
Além disso:
Utilizando e os valores calculados na expressão, a gente fica com:
Passo 6
Pelo balanço de energia:
Resposta
- O circuito térmico é dado abaixo:
- A taxa de calor máxima do chip deve ser: