O motor cilíndrico de uma moto é constituído por alumínio () e tem uma altura de com diâmetro de . Sob condições normais de operação, a superfície externa do cilindro encontra-se a uma temperatura de e é exposta ao ar ambiente, cuja temperatura vale e cujo coeficiente de convecção é . Aletas anulares são integradas ao corpo cilíndrico do motor para aumentar a transferência de calor para a vizinhança.

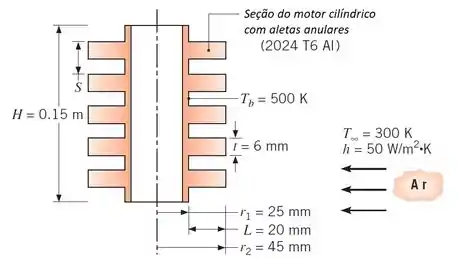
Considere cinco aletas anulares com espessura de , comprimento de e que estão igualmente espaçadas. Qual o aumento percentual na perda de calor ao utilizarmos as aletas?

Agora é a situação com as aletas! A taxa de calor trocada por um conjunto de aletas () é dada por:

Em que:

A área superficial de uma aleta anular é dada por:

A área total do sistema “aleta+base” é dada por:

Agora nos resta calcular o rendimento de uma aleta única (). Bora usar o gráfico (no capítulo anterior) pra isso:

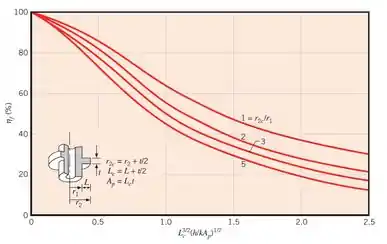
Então, a gente precisa calcular a razão entre e pra saber qual das quatro curvas usar e determinar o valor da abscissa!

Bora calcular o valor de x do gráfico então:

Em que e são calculados pelas expressões mostradas no gráfico:

Além disso:

Ufa! Agora a gente pode finalmente calcular o valor de x:

Pra saber qual das curvas serve pra gente, precisamos calcular a razão entre os raios:

Não tem nenhuma curva com esse valor, mas a gente pode colocar mais ou menos entre as curvas de razão igual a e , um pouco mais próximo da curva de .

Agora a gente já pode marca no gráfico a posição da abscissa e ver que a eficiência da aleta é aproximadamente:

Dessa maneira, é possível calcular a eficiência do sistema aletado e consequentemente a taxa de calor:

Substituindo os valores do enunciado:

Com as duas taxas calculadas a gente pode determinar o aumento percentual na perda e calor ao usarmos o sistema de aletas:

Esse valor é realmente relevante! Acho que ficou provado que as aletas ajudam bastante na troca de calor, não é mesmo?