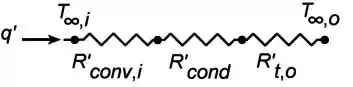
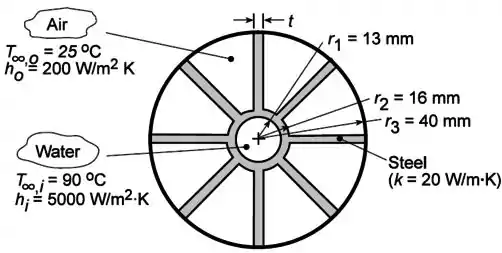
Um aquecedor de ar consiste em um tubo de aço () com raios interno e externo e respectivamente e oito aletas longitudinais integrais, cada uma com espessura . As aletas se estendem até um tubo concêntrico de raio , o qual tem sua face externa isolada. Água à temperatura escoa através do tubo interno enquanto o ar à temperatura de escoa através da região anular formada pelo tubo concêntrico maior.
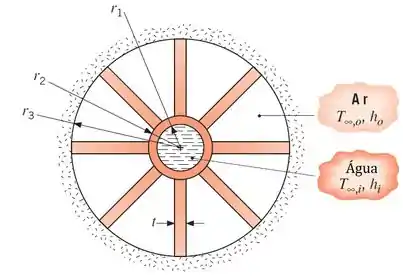
Esboce o circuito térmico equivalente do aquecedor e relacione cada resistência com os parâmetros apropriados do sistema.
Se e , qual é a taxa de calor por unidade de comprimento?
Passo 1
Esboce o circuito térmico equivalente do aquecedor e relacione cada resistência com os parâmetros apropriados do sistema.
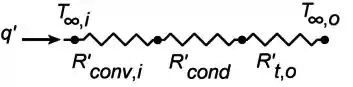
Em que:
Passo 2
Se e , qual é a taxa de calor por unidade de comprimento?
Pelo circuito térmico, a gente já sabe como escrever a taxa de calor que passa pelo sistema:
Bora calcular as resistências térmicas:
Passo 3
Para calcular a resistência térmica do sistema aletado, temos o seguinte:
Em que, representa a área de uma aleta sobre a unidade de comprimento e representa a área total do sistema aletado, inclusive a área da base que fica exposta.
Pra calcular essas áreas a gente pode considerar que o raio da superfície cilíndrica é muito maior que a espessura da aleta, então a gente pode admitir que a aleta é plana de seção retangular!
Bora lá! A gente tem que:
Sendo assim:
Agora só precisamos determinar a eficiência deste tipo de geometria de aleta (). Como as aletas são planas e retangulares, a gente tem o seguinte:
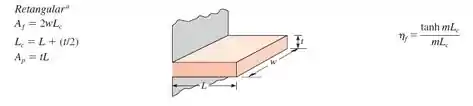
Em que:
Assim, temos que:
Dessa forma:
Passo 4
Agora a gente pode calcular a resistência térmica de contato do sistema aletado por:
E, finalmente, a taxa de calor por unidade de comprimento será:
Resposta
O circuito térmico é dado abaixo: