São colocadas 100 aletas em formato de disco igualmente espaçadas de em uma tubulação de de comprimento total. As aletas e a tubulação são de aço inoxidável 304.

Os discos possuem uma espessura de cada. A tubulação tem um diâmetro externo de e as aletas possuem de tamanho (diâmetro do disco da aleta é de ).

Admitindo que a temperatura da base (tubulação) seja de , qual é a quantidade de calor perdida para o ambiente considerando que o fluido ambiente está a e existe um coeficiente de película de .

Foi uma boa ideia colocar esse conjunto de aletas?

Assuma as propriedades termofísicas do aço inoxidável 304 constantes e iguais ao valor destas a .

Não é necessário desenvolver as soluções analíticas para esse problema. Utilize as informações previamente desenvolvidas e conhecidas.

A área superficial de uma aleta anular é dada por:

Onde:

Assim:

A área total do sistema “aleta+base” é dada por:

Precisamos agora calcular o rendimento de uma aleta única (). Para isso, vamos usar a seguinte equação:

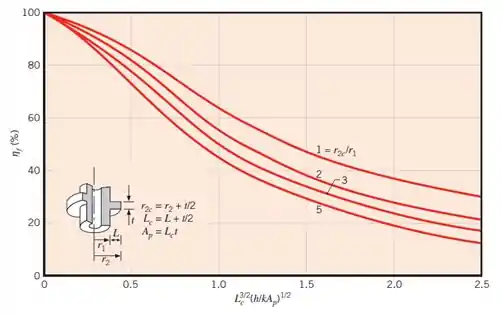
Onde:

Jogando esses valores na expressão da abscissa, onde :

Pra saber qual das curvas serve pra gente, precisamos calcular a razão entre os raios:

Como o valor de é muito grande, não temos como buscar exatamente o quanto vale a eficiência, então vamos estimar uma eficiência em torno de . Assim:

A eficiência global do sistema será:

Assim, a taxa de transferência de calor será:

Foi uma boa ideia colocar esse conjunto de aletas?

Caso não houvesse aletas, a taxa de transferência de calor, considerando o mesmo coeficiente convectivo seria:

Assim, como a ideia de um sistema aletado é aumentar a taxa de transferência de calor, foi uma boa ideia colocar esse conjunto de aletas, pois ele irá aumentar a taxa de transferência de calor.