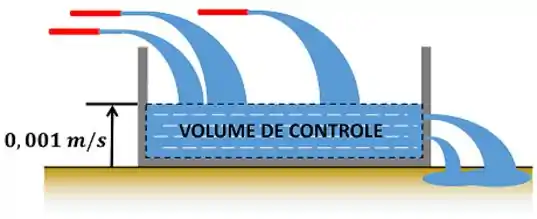
Uma piscina furada de base circular com de diâmetro está se enchendo de água por meio de três mangueiras. Por uma mangueira passa uma vazão volumétrica de , pelas outras duas passa uma vazão volumétrica de . A altura do nível da água sobe com uma velocidade constante de . Considerando que a água possui , determine a vazão mássica de saída da água. Suponha que a água vaza por dois furos com a mesma vazão mássica.
Passo 1
Enunciado pede para a gente calcular a vazão mássica de água que sai por um dos furos . Para resolver esse exercício precisamos usar a fórmula de conservação de massa.
onde:
- é o somatório da quantidade de massa que entra no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo ;
- é o somatório da quantidade de massa que sai no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo .
A figura abaixo mostra todas as informações que o enunciado nos dá para a gente conseguir fazer as contas que precisamos. Além disso ele mostra a incógnita do problema .
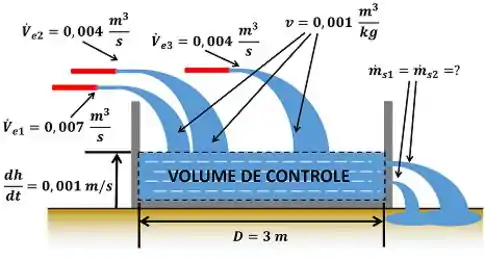
, e presentes na figura são as vazões volumétricas da água passando pelas mangueiras , e . e são as vazões mássicas de água que saem pelos dois furos e . é o volume específico da água. é a velocidade com a qual o nível da água sobe.

Ou seja, temos apenas as vazões volumétricas , mas precisamos das vazões mássicas .
No próximo passo aprenderemos a calcular as vazões mássicas a partir das vazões volumétricas e do volume específico . Além disso, vamos aprender a calcular a partir de .
Passo 2
Para converter vazão volumétrica e vazão mássica , é só multiplicar as vazões volumétricas por !
O da água pode ser calculado a partir do volume específico !
O somatório das vazões mássicas de entrada é a soma dessas três vazões mássicas.
As vazões mássicas de saída de água são iguais. Isso significa que o somatório das vazões de saída é igual ao dobro da vazão de um único furo .
O volume de água na piscina é igual à altura da piscina multiplicada pela área de sua base. A taxa de variação do volume da piscina é igual à taxa de variação da altura da piscina multiplicada pela área de sua base.
Todos esses dados estão presentes na figura.
Para converter para , multiplicamos pelo da água.
Com todas essas informações podemos criar uma fórmula para as vazões de saída.
Sabendo de tudo isso, vamos calcular as vazões de saída da água!
Passo 3
Primeiro vamos encontrar !
Em segundo lugar, calculamos a taxa de variação de volume de água da piscina .
Agora podemos calcular a vazão mássica de saída da água por um único furo através da fórmula que criamos.