Uma substância escoa nos tubos indicados na figura abaixo. Um tanque está conectado a esses tubos através de duas ramificações, cada uma com uma válvula. Abrem-se as válvulas e a substância enche o tanque com uma vazão volumétrica constante de em cada ramificação. Qual é a taxa de variação da massa do tanque? Considere que a massa específica dessa substância meça .
Passo 1
O exercício pede para a gente calcular a taxa de de variação da massa do tanque . Isso significa que precisamos calcular a quantidade de massa que entra no tanque por segundo. Fazemos isso através da fórmula abaixo. Ela mostra que o acúmulo de massa dentro do tanque é igual à quantidade de massa que entra menos a quantidade de passa que sai do tanque .
onde:
- é o somatório da quantidade de massa que entra no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo ;
- é o somatório da quantidade de massa que sai no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo .
A figura abaixo mostra todas as informações que o enunciado nos dá para a gente conseguir fazer as contas que precisamos. Além disso ele mostra a incógnita do problema .
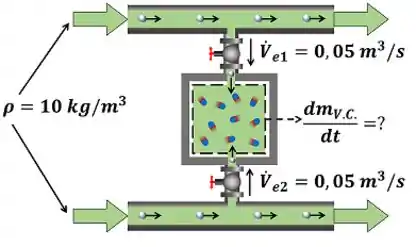
e presentes na figura são as vazões volumétricas da substância passando pelos tubos e . é a massa específica da substância.
Ou seja, temos apenas as vazões volumétricas , mas precisamos das vazões mássicas .
No próximo passo aprenderemos a calcular as vazões mássicas a partir das vazões volumétricas .
Passo 2
Para converter vazão volumétrica e vazão mássica , é só multiplicar as vazões volumétricas por !
O somatório das vazões mássicas de entrada é a soma dessas duas vazões mássicas.
Nesse exercício, vale zero, porque não tem nenhuma massa saindo do tanque. Tem apenas massa entrando!
Agora vamos para o cálculo final de .
Passo 3
Primeiro vamos encontrar as vazões mássicas e !
Com isso, dá pra calcular o somatório das vazões de entrada .
Substituindo esses valores na fórmula de , encontramos que: