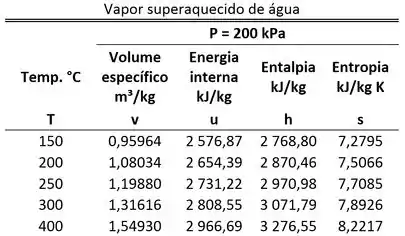
Uma substância escoa nos tubos indicados na figura abaixo. Um tanque com vapor d’água superaquecido está conectado a esses tubos através de quatro ramificações com seções transversais circulares. Cada ramificação possui uma válvula. Abrem-se as válvulas e o tanque esvazia através das ramificação e ao mesmo tempo em que enche através da ramificação e . O vapor d’água superaquecido sai pela ramificação com uma velocidade média de e entra pela ramificação com velocidade média de . Além disso, o vapor d’água superaquecido sai do tanque pela ramificação com uma velocidade média de e entra no tanque pela ramificação 4 com velocidade média de . Considere que a pressão do em todas as ramificações é igual a . As temperaturas do vapor d’água superaquecido nas ramificações , , e valem , , e respectivamente. Sabendo que os diâmetros das ramificações , , e valem , , e respectivamente, calcule a taxa de variação da massa de vapor d’água superaquecido no tanque.
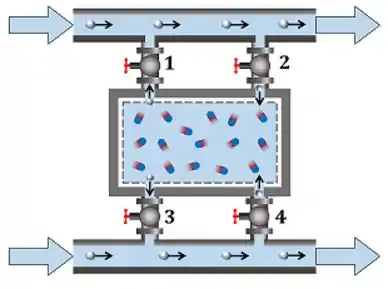
Use a tabela termodinâmica da água abaixo.
Passo 1
O exercício pede para a gente calcular a taxa de de variação da massa do tanque . Isso significa que precisamos calcular a quantidade de massa que sai do tanque por segundo. Fazemos isso através da fórmula abaixo. Ela mostra que o acúmulo de massa dentro do tanque é igual à quantidade de massa que entra menos a quantidade de passa que sai do tanque .
onde:
- é o somatório da quantidade de massa que entra no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo ;
- é o somatório da quantidade de massa que sai no volume de controle por segundo. Sua unidade no S.I. é o quilograma por segundo .
A figura abaixo mostra todas as informações que o enunciado nos dá para a gente conseguir fazer as contas que precisamos.
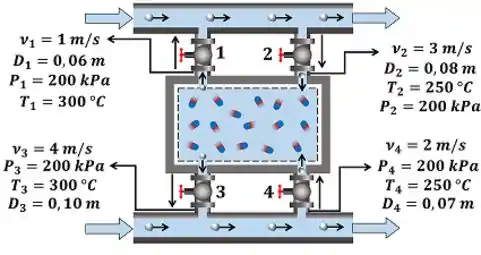
, , e presentes na figura são as velocidades do vapor passando pelas ramificações , , e . , , e são os diâmetros das ramificações , , e . , , e são as temperaturas do vapor que passa pelas ramificações , , e . , , e são as pressões do vapor que passa pelas ramificações , , e .

Ou seja, conhecemos as velocidades, os diâmetros, as temperaturas e as pressões do vapor, mas precisamos calcular a taxa de variação da massa de vapor no tanque . Para isso, vamos aprender a calcular as vazões mássicas a partir das velocidades , dos diâmetros e do volume específico . Portanto, precisamos primeiro saber achar o volume específico do vapor, usando a tabela de propriedades termodinâmicas da água.
Passo 2
Para achar os volumes específicos na tabela, temos que olhar para o valor de volume específico que está na mesma temperatura do vapor. A figura abaixo mostra onde estão os valores de volume específico do vapor que passa pelas quatro ramificações.
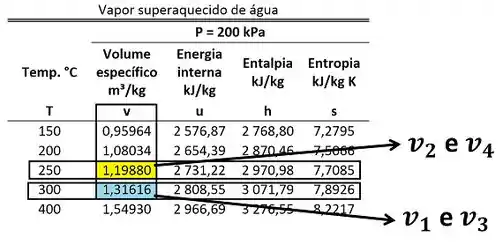
Agora precisamos que descobrir como se calcula as vazões mássicas com as informações que temos.
Passo 3
A primeira etapa para calcular através dos dados que nós temos é converter o valor de volume específico do ar em massa específica do vapor .
A segunda etapa é calcular as vazões volumétricas de vapor que passam por cada ramificação. Todas as vazões volumétricas são iguais à velocidade média do vapor multiplicada pela área da seção transversal da ramificação .
A terceira etapa é converter vazão volumétrica e vazão mássica . Para isso é só multiplicar as vazões volumétricas por !
O somatório das vazões mássicas de saída é a soma das vazões mássicas das ramificações e .
O somatório das vazões mássicas de entrada é a soma das vazões mássicas das ramificações e .
Sabendo disso, podemos calcualr pela fórmula de conservação de massa.
Passo 4
Iniciamos as contas, achando os valores de volume específico do vapor através da tabela e propriedades. Nela vemos que eles valem:
Agora sim podemos calcular . Para isso, calculamos primeiro .
Depois, achamos .
Por fim, encontramos .