Um série de placas de circuitos verticais encontra-se imersa em ar ambiente quiescente a . Embora os componentes sejam salientes em relação aos substratos, é razoável, em uma primeira aproximação, considerar placas planas com fluxo térmico na superfície uniforme .
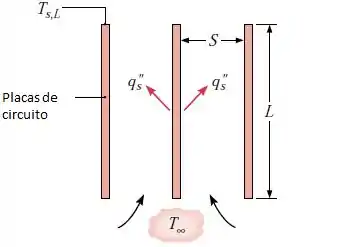
Considere placas com comprimento e largura e espaçamento . Se a temperatura máxima admissível na placa é de , qual é a potência máxima que pode ser dissipada por placa?
Passo 1
Esse é um problema de escoamento em canal vertical em que temos fluxo constante em ambas as placas, pra resolvê-lo vamos ter que utilizar a seguinte correlação para o número de Nusselt:
Onde é dado por:
Assim, vamos precisar pegar algumas propriedades do ar à temperatura de filme .
Agora podemos seguir em frente!
Passo 2
Substituindo os valores, o número de Rayleigh será dado por:
Substituindo na expressão do número de Nusselt, teremos:
Como estávamos trabalhando com uma situação em que as placas tem fluxos térmicos simétricos: e . Logo:
Show! Agora vamos tentar encontrar outra expressão para o número de Nusselt.
Passo 3
O número de Nusselt está associado ao coeficiente convectivo através da seguinte equação:
Esse mesmo coeficiente convectivo está associado ao fluxo de calor da seguinte forma:
Opa! Se substituirmos a expressão do coeficiente convectivo na expressão acima, teremos o seguinte:
Se reorganizarmos esse cara pra isolar o número de Nusselt, teremos:
Substituindo os valores:
Opa! Agora basta igualar as duas expressões pra encontrarmos o valor do fluxo térmico.
Passo 4
Agora não tem muito jeito, o fluxo térmico é calculado por tentativa e erro. Nesse caso, vamos encontrar que:
Passo 5
Pra fechar, como queremos calcular a taxa de transferência de calor, basta multiplicar o fluxo pela área das placas:
![]()