Um tanque cilíndrico de propano de de diâmetro e de comprimento é inicialmente cheio com propano líquido, cuja densidade é . O reservatório é exposto ao ar ambiente a em condições meteorológicas calmas.
A superfície externa do tanque é polida de modo que a transferência de calor por radiação é desprezível. Agora, uma rachadura se desenvolve na parte superior do tanque e a pressão no interior cai para enquanto a temperatura cai para , que é a temperatura de ebulição do propano a .
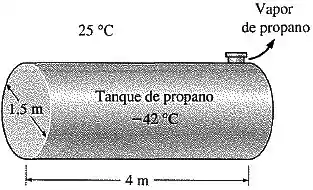
O calor de vaporização do propano a é . O propano é lentamente vaporizado como resultado da transferência de calor do ar ambiente para o reservatório e seu vapor escapa do tanque a através da rachadura.
Considerando que o tanque de propano está mais ou menos na mesma temperatura que o propano em seu interior, em qualquer momento, determine quanto tempo vai demorar para o tanque esvaziar se ele não estiver isolado.
Passo 1
Antes de qualquer coisa, vamos determinar as propriedade do ar à temperatura de filme, dada por:
De acordo com a tabela A.4 do Incropera, a essa temperatura:
Além disso, o coeficiente de expansão volumétrica térmica é dado por:
Passo 2
Inicialmente, temos uma massa de propano, dada por:
A massa de propano passa a evaporar a uma taxa , dada por:
Onde .
Onde e estão associados por:
Dessa brincadeira toda, o único cara que não temos é o coeficiente convectivo. Vamos atrás dele então.
Passo 3
O coeficiente convectivo é dado por:
Para cilindros, o número de Nusselt é dado por:
Onde o número de Rayleigh é dado por:
Substituindo os valores:
Substituindo na expressão do número de Nusselt:
Finalmente o coeficiente convectivo será:
Passo 4
Assim, a vazão mássica de propano será:
Onde:
Logo:
Passo 5
Finalmente, o tempo necessário pra esvaziar o tanque será:
![]()