Algumas das aplicações mais importantes do cálculo diferencial são os problemas de otimização, em que devemos encontrar a maneira ótima (melhor maneira) de fazer alguma coisa. Um bom jeito de achamos essa maneira é avaliando os pontos de máximo e mínimo da função que descreve nosso problema.
Encontre os máximos e mínimos relativos da função .
Passo 1
E aí, tudo bem?
Aqui a primeira coisa que vamos fazer, é derivar essa nossa função e depois igualar a nossa a zero para determinarmos os pontos críticos dela:
Usamos a regra do tombo aqui: :
Passo 2
Vamos igualar essa nossa a zero:
Pra resolver essa equação do segundo grau, vamos utilizar a fórmula de Bháskara:
Sendo que aqui temos: :
Passo 3
Encontramos as coordenadas de dos nossos pontos críticos.
Agora nos resta descobrir quem é mínimo e quem é máximo. Pra isso, vamos fazer o teste da derivada segunda:
Mais uma vez, vamos usar a regra do tombo:
Passo 4
O critério do teste da segunda derivada é o seguinte:
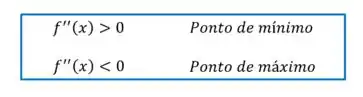
Vamos então calcular quanto vale a segunda derivada para os dois pontos críticos que encontramos:
Como a segunda derivada é positiva, é um ponto de mínimo.
Já para , como a segunda derivada é negativa, temos um ponto de máximo.
Passo 5
Pra finalizar, vamos encontrar os valores correspondentes da função para cada um dos pontos.
Para o ponto de mínimo, substituímos :
Para o ponto de máximo, substituímos :