Determine os intervalos onde a função abaixo cresce e decresce:
Passo 1
Fala aí!
A questão pede para encontrarmos os intervalos onde a função cresce e decresce, pra isso precisamos calcular sua derivada.
Isso porque a derivada representa a inclinação da reta tangente a função. Quando o gráfico de uma função está descendo a reta tangente a ele estará inclinada negativamente, e quando estiver subindo, sua tangente estará inclinada para cima.
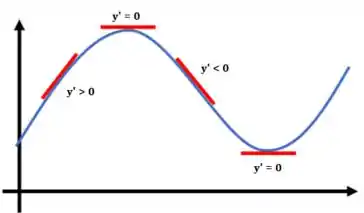
Então, nos intervalos onde a derivada da função for positiva , a função está crescendo e quando for negativa , está decrescendo.
Passo 2
Para começar, precisamos derivar a função:
Vamos usar a regra do peteleco
E lembrando que derivada de constante é zero, temos:
Passo 3
Agora, vamos montar a primeira inequação para encontrar o intervalo onde a derivada é positiva, ou seja, maior que zero:
Para tirarmos o sinal de negativo do , vamos multiplicar toda a inequação por , quando fazemos isso invertemos também o sinal de maior para menor:
Então, quando é menor que , a derivada é positiva e a função está crescendo!
Passo 4
Agora fazemos o mesmo processo, mas para encontrar o intervalo onde a derivada é negativa:
De novo, multiplicamos toda a expressão por :
Quando é maior que , a derivada é negativa e a função está decrescendo!
Se quisermos conferir se os intervalos que encontramos estão certinhos, podemos conferir o gráfico da função:
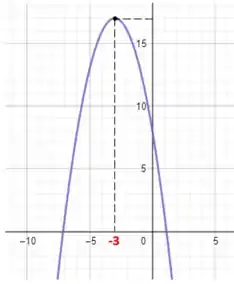
Como podemos ver, a função cresce antes de e depois decresce!
Resposta
A função cresce quando e decresce quando .