Seja a função . Determine o valor máximo assumido por essa função.
8
Passo 1
Bom, a questão pede pra encontrarmos o valor máximo assumido pela função, então precisamos encontrar os pontos críticos e checar se são de máximo ou mínimo.
Bora lá!
Passo 2
A primeira coisa a se fazer para encontrar os pontos críticos de uma função, é calcular sua derivada:
Usando a regra do peteleco, temos:
Passo 3
Os pontos críticos estarão nos pontos onde a derivada for igual a zero, vamos então igualar a derivada que encontramos a zero e resolver a equação formada:
Então, é o ponto crítico dessa função!
Passo 4
Agora precisamos conferir se esse é um ponto de máximo ou de mínimo, pra isso, vamos calcular a segunda derivada da função:
O critério é o seguinte:
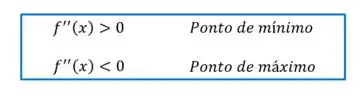
Como da nossa função é sempre negativa, o ponto crítico é um ponto de máximo, exatamente como queríamos!
Passo 5
Pra encerrar, a questão pediu o valor máximo assumido pela função, ou seja, queremos saber quanto vale a função no seu ponto máximo.
Vamos então calcular para :
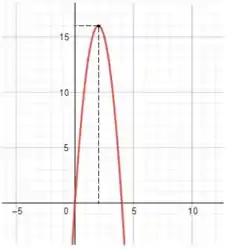
Então, o valor máximo assumido pela função quando é .
Se traçarmos o gráfico da função, conseguimos ver direitinho: