Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Crescimento, Decrescimento, Máximos e Mínimos

Ver Teoria
Exercício 81234567910

Enunciado

Encontre os pontos de inflexão da curva f x = 3 x 4 - 10 x 3 - 12 x 2 + 12 x - 7 .

Passo 1

Pra ter uma ideia do que estamos falando, um ponto de inflexão é uma coisa como essa:

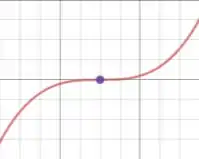
Pondemos dizer que é o ponto onde a função muda de comportamento. Repara que ela tinha uma cruva com concavidade para baixo, indicando um crescimento que ia mais devagar a cada passo, e no ponto azul ela passou a ter uma concavidade para cima, indicando um crescimento que vai cada vez mais rápido.

E matematicamente falando, como podemos achar esse ponto? Bom, esse é um ponto crítico onde a segunda derivada da função vale zero. Ou seja

f ' ' x = 0

Passo 2

Vamos calcular as duas derivadas:

f x = 3 x 4 - 10 x 3 - 12 x 2 + 12 x - 7

Lembra que a derivada da soma é o mesmo que a soma das derivadas? Ou seja

f ' x = 3 x 4 - 10 x 3 - 12 x 2 + 12 x - 7 '

= 3 x 4 ' - 10 x 3 ' - 12 x 2 ' + 12 x ' - 7 '

Agora vai ser só calcular cada uma dessas derivadas aí. Pra derivada de polinômio temos

x n ' = n ∙ x n - 1

Lembrando que a derivada da constante vale zero, certo? Logo a derivada daquele 7 ali vai ser nula...cuidado.

= 3 x 4 ' - 10 x 3 ' - 12 x 2 ' + 12 x ' - 7 '

= 4 ∙ 3 x 3 - 3 ∙ 10 x 2 - 2 ∙ 12 x 2 + 12 x 0

f ' x = 12 x 3 - 30 x 2 - 24 x + 12

E agora fazemos o mesmo processo pra segunda derivada

f ' ' x = 3 ∙ 12 x 2 - 2 ∙ 30 x - 24 x 0

f ' ' x = 36 x 2 - 60 x - 24

Passo 3

Vamos começar achando os pontos que tem derivada segunda igual a zero:

f ' ' x = 0

36 x 2 - 60 x - 24 = 0

Vamos dividir tudo por 12 pra deixar nossas contas mais simples. Atenção na matemática aqui. Lembra que numa equação, tudo o que fazemos de um lado, temos que também fazer no outro pra mantermos a igualdade, certo? Então

36 x 2 - 60 x - 24 12 = 0 12

3 x 2 - 5 x - 2 = 0

Como é uma equação de segundo grau, podemos usar Bháskara fazendo:

Δ = b 2 - 4 a c

x = - b ± Δ 2 a

Detalhe, no nosso caso temos

a x 2 + b x + c = 0

a = 3 ,   b = - 5 ,   c = - 2

Vamos jogar nas fórmulas então. Primeiro calculando o delta

Δ = - 5 2 - 4 ∙ 3 ∙ ( - 2 )

= 25 + 24 = 49

x = 5 ± 49 6 = 5 ± 7 6

Ou seja, temos duas raízes:

x 1 = 5 + 7 6 = 2

x 2 = 5 - 7 6 = - 1 3

Passo 4

Beleza, descobrimos as coordenadas x dos pontos de inflexão, e pra descobrir as coordenadas y vamos jogar esses valores de x na função

f x = 3 x 4 - 10 x 3 - 12 x 2 + 12 x - 7

  • Para x = 2

    • f 2 = 3 ( 2 ) 4 - 10 2 3 - 12 2 2 + 12 ( 2 ) - 7 = - 63

    E o primeiro ponto é ( 2 , - 63 )

  • E para x = - 1 3

f x = 3 x 4 - 10 x 3 - 12 x 2 + 12 x - 7

f - 1 3 = 3 - 1 3 4   - 10 - 1 3 3 - 12 - 1 3 2 + 12 - 1 3 - 7

f - 1 3 = 3 81 + 10 27 - 12 9 - 11 = 3 + 30 - 108 81 - 11 = - 75 81 - 11 = - 322 27

E o segundo ponto é - 1 3 , - 322 27 .

Prontinho, achamos os pontos de inflexão.

Resposta

Os pontos de inflexão são - 1 3 , - 322 27 e ( 2 , - 63 ) .