Determine os pontos da função , nos quais as retas tangentes são horizontais.
Passo 1
Antes de tudo, precisamos lembrar que a derivada de uma função é representada pela inclinação da reta tangente ao gráfico daquela função em determinado ponto:
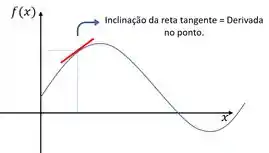
Como o enunciado tá dizendo que a reta tangente é horizontal, ela não terá inclinação e vai ficar tipo assim no gráfico:
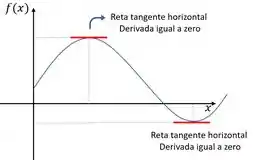
Em outras palavras, a derivada será igual a zero. E o que ele está querendo saber é qual é o ponto que faz isso acontecer. Repara que isso acontece quanto a função tem seus valores máximos e mínimos, também chamado de pontos críticos.
Então pra descobrir esses valores de , vamos precisar derivar essa nossa função e igualar a zero. Partiuuu!!!
Passo 2
Começamos pela derivada:
Lembra que temos a propriedade em relação a soma, onde podemos calcular a derivada de cada termo
Pra essa vamos fazer a regra do peteleco e não mexemos na constante, certo?
A próxima derivada vai ser no mesmo esquema da anterior, regrinha do peteleco e não mexemos na constante
O último é a derivada de uma constante, que é zero
Logo
Passo 3
Igualando a zero, teremos
Virou uma equação que podemos resolver isolando o , jogando o que está subtraindo, para o outro lado.
Agora é a vez de jogar o 3 que tá multiplicando, para o outro lado dividindo:
Temos:
Agora a pergunta é: Qual o valor que quando elevado ao quadrado dá 4?
Há duas possibilidades:
Porque ambos elevados ao quadrado resultam em
Passo 4
Agora vamos substituir esses valores na nossa função original
Primeiro para
Ou seja, o primeiro ponto é formado pelas coordenadas .
Agora vamos fazer para o
Ou seja, o segundo ponto é