Seja . Determine o(s) intervalos onde a função é decrescente
(a)
(b) Nenhuma das respostas
(c)
(d)
(e)
Passo 1
Opa! Tudo joia?
Olha só: uma função é decrescente nos pontos em que a sua derivada é negativa. Veja o exemplo desse gráfico aqui:
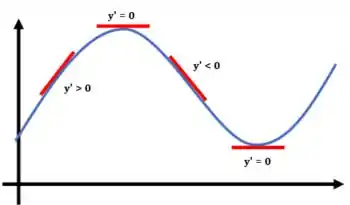
Vamos achar a derivada de então!
A gente vai usar a regra do tombo, beleza?
Essa aqui:
Passo 2
Aplicando essa regra na nossa função, fica assim:
(Lembra que derivada de constante é zero e que 😊)
Passo 3
A gente quer os pontos onde a derivada é negativa, ou seja:
Vamos resolver essa inequação, então!
Pra tirar esse quadrado do , podemos colocar raiz quadrada dos dois lados da equação:
Mas quando fazemos isso, precisamos colocar um módulo no :
Passo 4
Pra finalizar, vamos lembrar que o módulo pode ter dois resultados, positivo ou negativo:
Como nessa segunda temos um , pra deixá-lo positivo, nós multiplicamos tudo por , o que no final das contas, vai mudar o sinal de todo mundo, incluindo o sinal de que vai virar :
Com isso, temos que:
- ( é maior que )
- ( é menor que
Com isso, o intervalo onde a derivada é negativa é entre e , que escrevendo em matematiquês fica:
E esse é o intervalo onde a função é decrescente! 😊