Determine qual(is) são os pontos críticos da função .
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala aí, tudo joia?
Olha só, ponto crítico é onde a derivada é zero, beleza?
Isso porque a derivada é a inclinação da reta tangente ao gráfico. Um ponto crítico é um ponto onde a função atinge seu valor máximo ou mínimo, nesses pontos a reta tangente fica completamente na horizontal. Sendo assim, ela não terá nenhuma inclinação, e por isso a derivada será igual a zero.
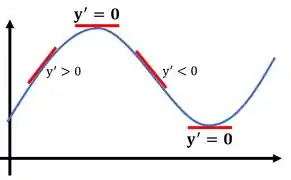
Vamos começar calculando a derivada então...
Passo 2
Vamos derivar essa função aqui:
A gente tem um polinômio, então vamos derivar usando a regra do Tombo, lembra dela?
Vamos aplicar isso na nossa função!
Passo 3
Aplicando a regra do Tombo na função , temos:
A gente ainda pode colocar o em evidência:
Passo 4
Agora que já achamos a derivada, vamos ver em que ponto ela é igual a zero, fazendo:
Pra um produto dar zero, um dos fatores tem que ser zero, como aqui temos o multiplicando o , podemos ter essas duas condições:
Resolvendo essa segunda equação...
Passo 5
Beleza! Achamos os dois pontos críticos então, que são:
E é só isso por aqui😊
Resposta
(d)