Aplicando os conceitos de derivada, qual o gráfico da função definida em por ?
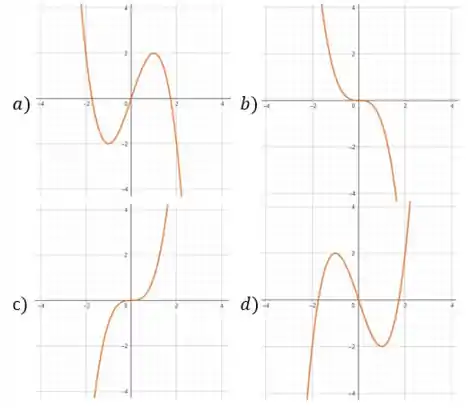
Passo 1
E aí, tudo beleza?
Vamos ver qual é o gráfico dessa função aqui:
Bom, o exercício falou pra a gente usar os conceitos de derivada. A gente sabe que com a derivada podemos achar os pontos de máximo e mínimo da função, bem como os intervalos de crescimento e decrescimento. Bora lá então?
Passo 2
Bora derivar a função então! A gente vai usar a regra do tombo: .
Aplicando em :
Passo 3
Bom, os pontos críticos da função, que são nossos candidatos a ponto de máximo e mínimo são os pontos onde a derivada é zero. Vamos ver isso igualando a derivada que acabamos de encontrar a zero, então:
Beleza! Esses são os pontos críticos da função😊
Passo 4
Vamos checar então se esses pontos críticos são de máximo ou de mínimo!
Pra isso, precisarmos fazer o teste da segunda derivada, que vamos calcular usando a regra do tombo mais uma vez e lembrando que derivada de constante dá zero:
Passo 5
Pelo teste da segunda derivada, temos:
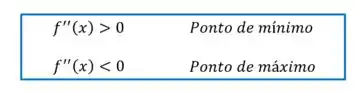
Vamos então calcular quanto vale pra cada um dos pontos críticos que encontramos:
Como é negativo quando , temos um ponto de máximo.
Como é positivo quando , temos um ponto de mínimo.
Passo 6
Agora vamos voltar aos gráficos e procurar qual deles possui um máximo em e um mínimo em .
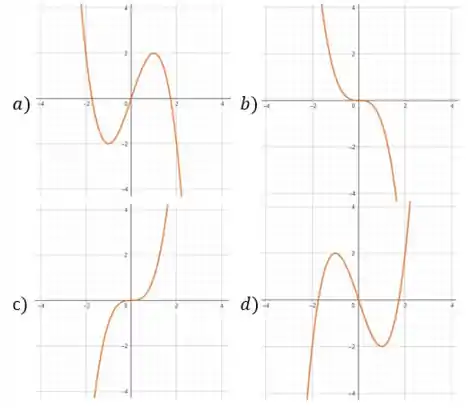
O único gráfico correspondente aos pontos que encontramos é o da alternativa , que é nossa resposta final!