Determine os intervalos onde a função abaixo cresce e decresce:
Passo 1
E aí, tudo bom?
Queremos encontrar os intervalos onde a função cresce e decresce e vamos fazer isso usando derivadas!
Pra isso, precisamos lembrar que a derivada representa a inclinação da reta tangente à função. Quando o gráfico de uma função está descendo, a reta tangente a ele estará inclinada pra baixo, e quando estiver subindo, sua tangente estará inclinada para cima.
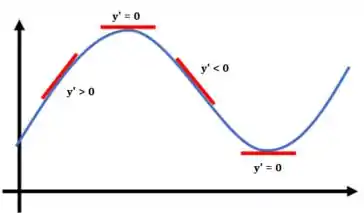
Então, nos intervalos onde a derivada da função for positiva , a função está crescendo e quando for negativa , está decrescendo.
Passo 2
Para começar, precisamos derivar a função:
Vamos usar a regra do peteleco
E lembrando que derivada de constante é zero, temos:
Passo 3
Precisamos descobrir os intervalos onde essa função é positiva e negativa, como temos uma função do 2º grau, vamos fazer um esboço do gráfico.
Primeiro, vamos descobrir as raízes, ou seja, os pontos onde a função é igual a zero:
Pra facilitar nossas contas, vamos dividir toda a expressão por :
Agora, vamos resolver usando a fórmula de Bhaskara:
Identificando os termos da nossa equação:
Substituindo na primeira fórmula:
Seguindo pra segunda:
Assim sendo, temos:
Então, as raízes da equação são e .
Passo 4
Para esboçar o gráfico, precisamos saber se a concavidade é pra cima ou pra baixo. Isso é definido pelo coeficiente da função do 2º grau: quando , temos concavidade para cima, e quando , temos concavidade para baixo.
Olhando para a derivada:
Temos , então a concavidade é para cima.
Passo 5
Finalmente, podemos fazer o esboço do gráfico, traçando uma parábola que passa pelos pontos e no eixo e que tenha concavidade para cima.
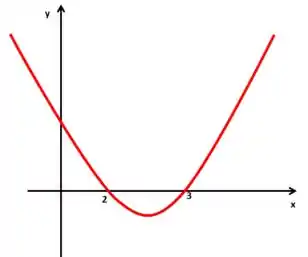
Olhando pro nosso esboço podemos ver que a derivada só é negativa no intervalo entre e , tanto pra , quanto pra , a derivada é positiva.
Como a função decresce quando a derivada é negativa, temos a função decrescendo para entre e .
E como a função cresce quando a derivada é positiva, temos a função crescendo para ou para .
Intervalos encontrados! Prontinho!
Resposta
A função cresce quando ou , e decresce quando .