O anel está firmemente ajustado ao eixo e deve ser removido do eixo pelo dispositivo de remoção mostrado. O parafuso tem uma rosca quadrada simples com um diâmetro médio de e um passo de . Se um torque de é necessário para girar a roda de forma a retirar o anel do eixo, determine a pressão média (tensão compressiva) entre o anel e o eixo. O coeficiente de atrito para o parafuso em vale e o do eixo e do anel vale . O atrito na extremidade esférica do eixo pode ser desprezado.
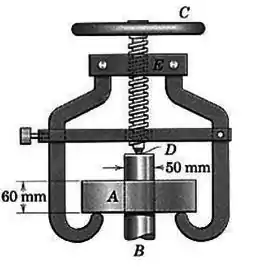
Passo 1
Para calcular o momento necessário para apertar o parafuso, temos que usar a seguinte fórmula:
Então, vamos começar calculando o ângulo de hélice ():
O passo do parafuso () vale e o raio vai ser a metade do diâmetro que foi dado no enunciado:
Então, o ângulo de hélice () será:
Passo 2
Sabendo que o coeficiente de atrito () vale , vamos ter que o ângulo de atrito () será:
Passo 3
Neste caso nós sabemos que o momento vale e queremos saber a força axial , então vamos ter que:
Passo 4
Agora precisamos saber a pressão . Para isso, temos que saber que a pressão é calculada por:
Onde, o coeficiente de atrito do eixo e do anel é e é a área de contato entre o anel e o eixo:
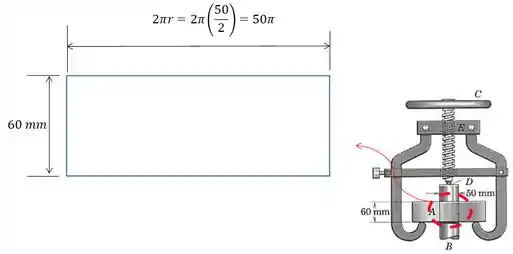
Então, a pressão será: