Especifique o torque necessário no parafuso motorizado para vencer a resistência de ao movimento do carro ao longo do seu trilho horizontal. O parafuso tem diâmetro médio de e tem duas roscas quadradas separadas que movem o carro por revolução do parafuso. O coeficiente de atrito vale .
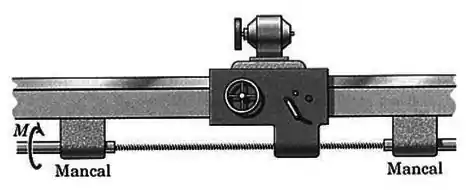
Passo 1
Para calcular o momento necessário para o parafuso vencer a resistência, temos que usar a seguinte fórmula:
Então, vamos começar calculando o ângulo de hélice ():
O passo do parafuso () nada mais é do que a distância que o parafuso percorre em uma volta, então vale . E o raio vai ser a metade do diâmetro que foi dado no enunciado:
Então, o ângulo de hélice () será:
Passo 2
Sabendo que o coeficiente de atrito () vale , vamos ter que o ângulo de atrito () será:
Passo 3
Sabendo que o parafuso precisa vencer uma carga de , então o momento necessário será: