Se o coeficiente de atrito entre a cunha de aço e as fibras úmidas de um tronco recentemente cortado vale , determine o ângulo máximo que a cunha pode ter para não pular fora da madeira após ter sido atingida pela marreta.
Passo 1
O sistema pode ser descrito assim:
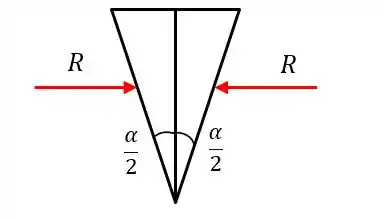
Para que a cunha seja auto-travante, devemos ter:
No caso limite, teremos:
Assim:
Resposta
Exercícios de Livros Relacionados
No sacador de engrenagensmostrado na figura, o parafuso de rosca quadrada A B tem um raio médio de 15m m e um avanço de 4m m . Sabendo que o coeficiente de atrito estático é 0,10 , determine o torque
No sacador de engrenagensmostrado na figura, o parafuso de rosca quadrada A B tem um raio médio de 15m m e um avanço de 4m m . Sabendo que o coeficiente de atrito estático é 0,10 , determine o torque
Na morsa de bancada mostrada, o mordente móvel D está rigidamente ligado a lingueta A B que se encaixa com folga no corpo fixo da morsa. O parafuso de rosca simples é rosqueado na base fixa e tem um d
Considerando no Problema 8.70 que uma rosca à direita seja usada em ambas as barras A e B , determine a intensidade do torque que deve ser aplicado à luva a fim de girá-la.
Determine a menor força vertical P exigida para empurrar o calço entre os dois cilindros idênticos, cada um com peso W . O coeficiente de atrito estático em todas as superfícies de contato é μ s = 0 ,