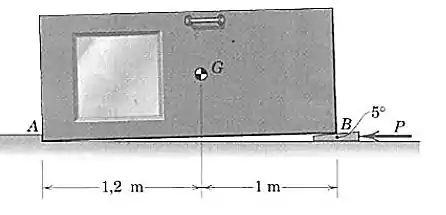
A porta industrial de e centro de massa em está sendo posicionada para reparo por meio da inserção de uma cunha de sob o canto . O movimento horizontal é impedido pelo pequeno degrau no canto Se os coeficientes de atrito estático nas superfícies superior e inferior da cunha valem , determine a força necessária para levantar a porta em
Passo 1
Vamos primeiro desenhar o sistema de forças na cunha:
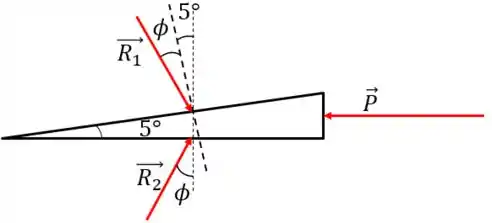
Vamos seguir uma estratégia: primeiro encontrar , depois vamos passar um eixo especial e decompor a força e nessa direção, achando, assim, o valor de
Passo 2
Vamos expandir um pouco o desenho de modo que possamos ver um pedaço da porta:
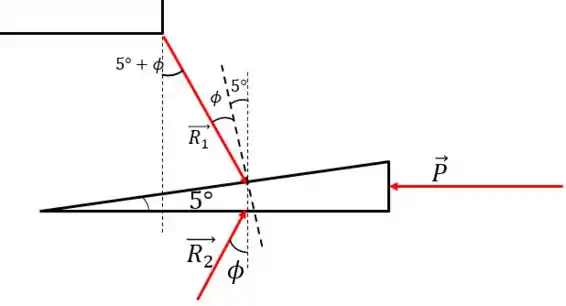
Perceba que o ângulo que a força faz com a aresta da porta é:
Mas quanto vale Este é o ângulo de atrito, sendo assim:
Agora vamos desenhar a nossa porta e as forças que atua nela:
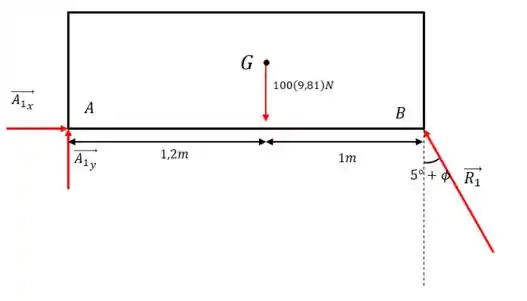
Como a porta exerce uma força na cunha, a cunha exerce a mesma força na caixa, certo?
Então, vamos usar o equilíbrio de momentos com relação ao ponto para calcularmos o valor de Fazer o momento com relação a este ponto nos ajuda porque assim eliminamos as forças em
Vamos achar as componentes da força :
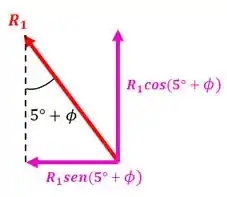
Perceba que o braço de alavanca com relação ao ponto é:
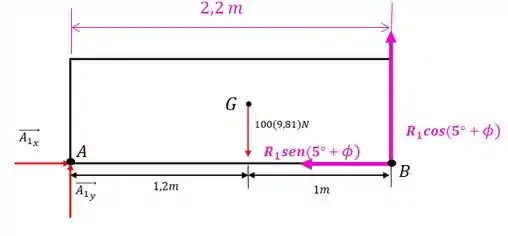
Pronto, agora podemos fazer o somatório de momentos com relação ao ponto :
Então, o valor de é:
Passo 3
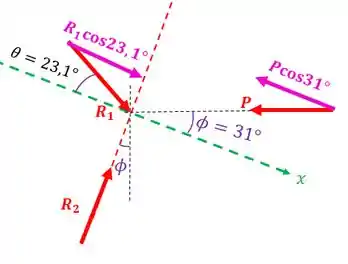
Vamos traçar um eixo especial, perpendicular à linha de ação de e marcar os ângulos:
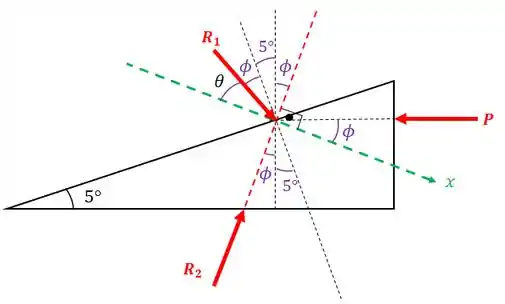
Vamos marcar melhor os ângulos:
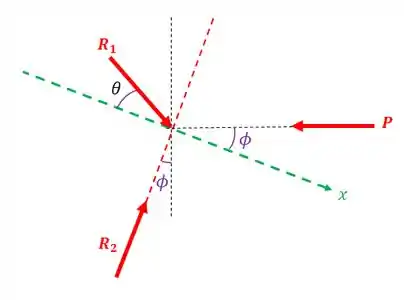
O ângulo entre e o eixo é , pois existe um ângulo de entre esse ângulo e o outro ângulo (que é aquele faz com a vertical)!!!
E
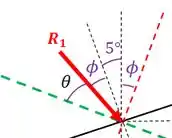
Olhando esse grupamento de ângulos, percebemos que a soma dos mesmos tem que dar . Assim:
Lembrando que :
Passo 4
Agora basta a gente fazer o equilíbrio das forças nesse eixo que criamos. Mas para isso temos que decompor as forças neste eixo: