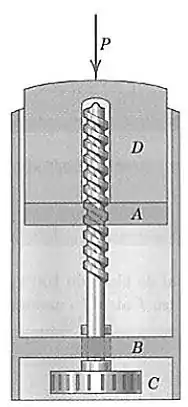
Os elementos de um tubo de desodorante em barra são mostrados na figura. Para subir a barra de desodorante o disco é girado. O eixo rosqueado se conecta as roscas de base móvel o eixo não tem roscas no suporte fixo . A rosca quadrada dupla de de diâmetro tem um passo de Determine o coeficiente de atrito estático , para o qual o desodorante não descerá sob a ação da força . Despreze o atrito em
Passo 1
Queremos saber o coeficiente de atrito mínimo para que o parafuso não se solte. Nesse caso, o parafuso não está ainda solto, mas sim no limiar do desparafusamento.
Então, basta a gente lembrar que na condição limite do desparafusamento:
Onde:
E é:
Passo 2
Sabemos que:
A rosca tem um diâmetro de , então o seu raio é de . E o passo foi dito no enunciado que é de . Sendo assim: