O coeficiente de atrito estático , entre o corpo de e a cunha com ângulo de vale Determine o módulo da força necessária para levantar o corpo de se:
- Rolamentos com atrito desprezível estejam colocados sob a cunha como mostrado.
- Os rolamentos sejam removidos e o coeficiente de atrito estático seja válido para essa superfície também.
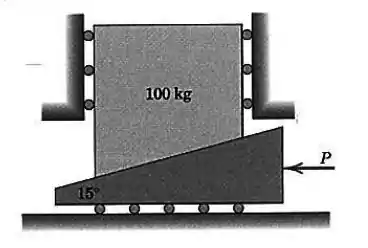
Passo 1
A presença dos rolamentos indica que não existe atrito na parte inferior da cunha.
Podemos, então, desenhar o sistema de forças na cunha como sendo esse:
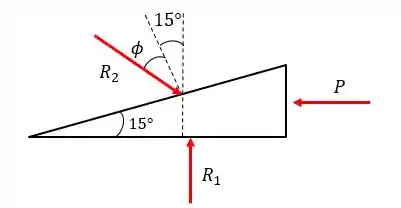
Perceba que a resultante é perpendicular e não inclinada neste caso, pois não existe atrito na parte de baixo da cunha.
Então, o ângulo de atrito é:
Olhando para o equilíbrio horizontal desse sistema, podemos achar uma relação entre e .
Mas antes temos que achar a componente horizontal da força :
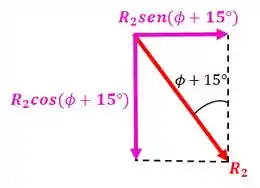
Então:
Passo 2
Agora vamos olhar para o corpo:
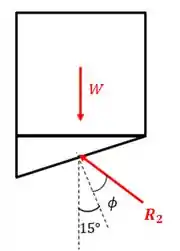
Olhando para o equilíbrio vertical, temos:
Onde é o peso e seu módulo vale:
E sabendo que:
Substituindo esse valor na expressão do equilíbrio vertical, temos:
Passo 3
Agora existe atrito entre a base da cunha e o chão. Com isso, algumas coisas mudarão, mas outras não!!!
Vamos olhar primeiro para o corpo:
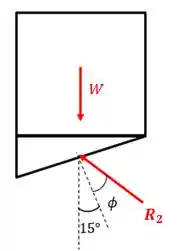
Os valores dos ângulos não mudaram, certo?
E nem peso mudou!
Então, o valor de também não mudou. Podemos calcular esse valor da mesma forma que vimos antes:
Agora, voltando para o equilíbrio da cunha, vemos um cenário diferente:
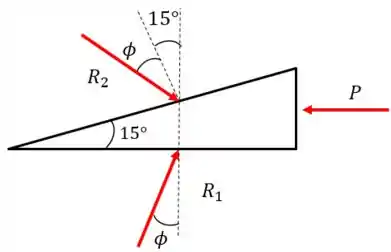
Como você pode ver, agora existe um ângulo entre a reação e a superfície da cunha devido ao atrito. Temos que aplicar o equilíbrio vertical para achar o novo valor de
Mas antes temos que achar as componentes verticais dessas forças que estão inclinadas:
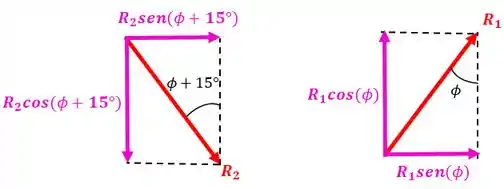
Então, o nosso equilíbrio vertical fica:
Agora, aplicando o equilíbrio horizontal: