Construa em Matlab o gráfico da função dada e da sua derivada:
Sob o intervalo
Passo 1
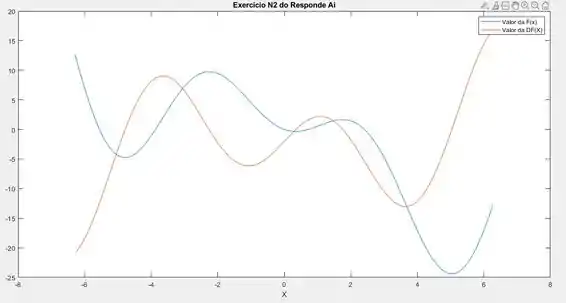
A questão em si está querendo simplesmente imprimir os valores da função e da sua derivada sob a variação de X, mas não em forma de uma tabela e sim na forma gráfica em um único gráfico.
Para tirar a derivada basta utilizarmos as variáveis simbólicas para obter a derivada, uma vez que temos a derivada em mão, iremos para a criação do código precisamos criar o algoritmo para entender o que o código faz:
- Entrada de dados, aqui implementa o valor de X.
- Cálculo da função de X
- Plotagem da função
- Nomeando os eixos e o título do gráfico.
Passo 2
Primeiro passo é a obtenção da derivada, para isso no commad window vamos criar a variável simbólica X.
Uma vez que criamos a variável simbólica vamos implementar a função
Agora que implementamos a função simbólica vamos tirar a derivada da função
E iremos obter a seguinte função derivada:
Passo 3
Primeiro passo é a criação do vetor de entrada:
Uma vez que criamos o vetor vamos calcular os valores da função e sua derivada:
Iremos chamar o plot da função e sua derivada:
E finalizamos formatando os eixos do gráfico:
E para organizar melhor vamos colocar a legenda no gráfico:
Passo 4
Implementando o código no matlab ele fica da seguinte forma:

Executando o código podemos obter a seguinte curva:
Resposta
Ei, a resposta está no passo a passo :)