Esboce o gráfico seguinte função:
No intervalo
Perceba que a função é descontínua em . Plote a função criando dois vetores no domínio O primeiro vetor terá elementos de até e o segundo vetor terá elementos de até
Passo 1
Opa galerinha, essa é uma questão típica de função bidimensional. Aqui nós temos uma variável dependente que é o em função de uma variável independente que é o , caracterizando uma curva bidimensional no Matlab.
Para gerar uma curva desse tipo utilizamos a função que é a função responsável por imprimir uma saída de dados gráfica.
Só que para utilizá-la iremos precisar de no mínimo dois vetores. Um vetor que corresponde ao eixo das ordenadas e segundamente vamos precisar de um vetor que será o eixo das abscissas.
Porém, essa questão aqui tem uma limitação. Essa função não está definida para valores de pois, analisando a função vemos que aparece uma divisão por 0 gerando assim uma indeterminação.
Para fugir desse problema vamos dividir o intervalo grande que é de até em dois intervalos pequenos excluindo o para assim remover a indeterminação.
Os valores de incrementos podem ser escolhidos de forma arbitrária eu irei utilizar 0,01 mas você pode utilizar qualquer um, certo?
Sendo assim, nosso algoritmo fica:
1-Criação do vetor x1,
2-Criação do vetor x2,
3-Cálculo do vetor y1,
4-Cálculo do vetor y2,
5-Plotagem da curva.
Passo 2
Agora que criamos o algoritmo basta transformá-lo em um programinha do Matlab, as primeiras linhas de código são apenas as criações dos vetores, logo:
Agora vamos criar os vetores calculando as funções nesses intervalos, lembre-se que estamos realizando o cálculo da função em cada elemento do vetor , então precisamos colocar o antes da operação para indicar isso.
Até aqui tá tudo okay, agora vamos para a novidade.
Passo 3
A função plot precisa de dois argumentos, o primeiro argumento é o eixo das abscissas e o segundo argumento é o eixo das ordenadas. Ou seja, sempre que for plotar precisamos colocar no primeiro argumento o vetor que corresponde os valores de e depois os valores do eixo .
Porém temos dois gráficos, né?
Então para inserir o segundo gráfico basta continuar, primeiro inserimos os valores do eixo x do segundo gráfico e depois inserimos os valores do eixo y do segundo gráfico.
Inserindo tudo certinho seu código deve ficar assim:
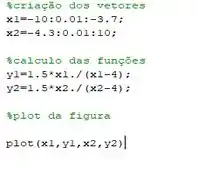
O executando sua curva deve ficar algo mais ou menos assim:
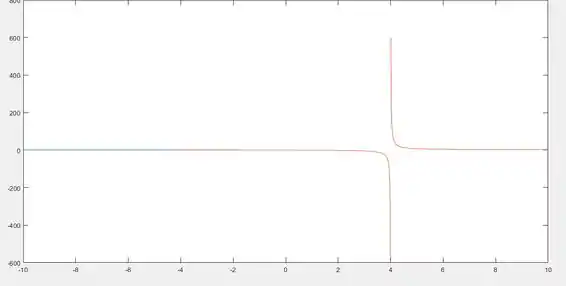
Resposta
Ei, a resposta está no passo a passo :)