Um resistor e um indutor são conectados em série com uma fonte de tensão. Quando a fonte de tensão produz pulsos regulares de amplitude 12 V e duração 0.5s.
A corrente do que passa no circuito é modelada pelas seguintes funções:
E
Plote em um único gráfico ambas as curvas para uma melhor visualização do comportamento físico do sistema.
Passo 1
A questão pede pra gente estudar a variação da corrente em um circuito RLC, a ideia aqui é estudar o que acontece com a corrente quando existe uma variação no tempo.
Porém, a função que modela a corrente muda conforme o tempo avança.
Sendo assim, o nosso plot irá possuir duas curvas. A primeira curva irá corresponder a corrente para valores de tempo até os 0.5 segundos.
Depois de 0.5 segundos iremos utilizar a segunda função e então iremos implementar uma segunda curva no mesmo gráfico.
Lembrando alguns detalhezinhos, o Matlab de certa forma ele não plota uma curva contínua, na realidade ele calcula a função que queremos em diversos pontinhos e gera um gráfico com esses pontinhos um do lado do outro. Quando esse gráfico aparece na nossa tela do computador, esses pontinhos ficam tão próximos um do outro que dá a impressão que é uma curva contínua. Na verdade, a gente plota vetores com pontos da função e não a própria função!
Então para os pontos ficarem pertinhos um do outro e melhorar nossa precisão, geralmente, se define os incrementos na ordem de 0.01.
Então precisamos indicar quais são esses pontos onde a função irá calcular o seu valor, belezinha?
Sendo assim, o algoritmo da rotina vai ser da seguinte forma:
1-Entrada de dados: V,R e L
2- Cálculo da função
t1=0:0.01:0.5
t2=0.5:0.01:1
Cálculo da função i1
Cálculo da função i2
3-Implementação do gráfico
4-formatação da curva
Passo 2
Como mostra no algoritmo, primeiramente devemos criar os dados de entrada.
E criar os vetores de tempo.
Calculando os valores das correntes:
Agora iremos fazer o plot da corrente em função do tempo, como nós temos dois vetores de tempo e dois vetores de corrente para plotar precisamos indicar os pares na ordem correta.
Como os valores da função corresponde aos valores do vetor temos que a função plot fica:
Agora precisamos indicar os pares correspondente a segunda curva que irá aparecer no gráfico, para isso vamos utilizar os pares e seus valores de correspondente e só precisamos fazer a seguinte modificação no plot:
E lembrando sempre, primeiramente se colocar os valores do eixo X que nesse caso é o tempo, depois coloca-se os valores do eixo Y que nesse caso é os valores das correntes, belezinha?
E agora finalizamos formatando os eixos do gráfico:
Passo 3
Executando o código podemos obter a seguinte curva:
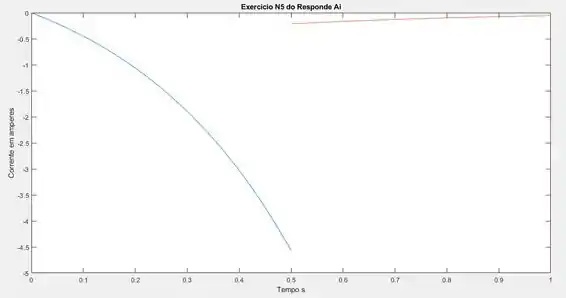
Resposta
Ei, a resposta está no passo a passo :)