A órbita dos planetas ao redor do sol pode ser modelada aproximadamente pela equação polar.
Os valores das constantes e para quatro planetas são mostradas abaixo:
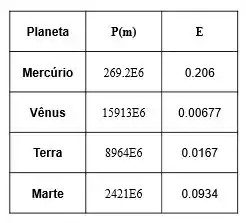
Plote as órbitas dos planetas apresentados em função de teta, todos em um único gráfico.
Passo 1
A questão em si pede para modelar as órbitas dos planetas Mercúrio, Vênus, Terra e Marte.
Onde a ideia é utilizar os dados fornecidos na questão e variar o ângulo teta de 0 até para assim calcular os valores dos raios de todas as órbitas e imprimir os resultados em uma curva bidimensional.
Então o algoritmo se torna:
1-Implementação da entrada de dados:
2-Cálculo dos raios
3-implementação do plot
4-formatação da curva.
Passo 2
Primeiro passo é a criação dos vetores de entrada no Si:
Cálculo dos raios dos planetas
Agora iremos chamar o plot da tensão em função da deformação
E finalizamos formatando os eixos do gráfico:
Passo 3
Executando o código podemos obter a seguinte curva:
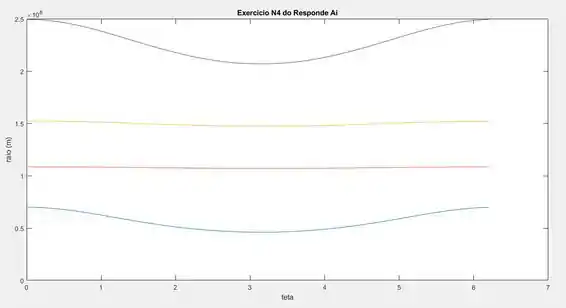
Resposta
Ei, a resposta está no passo a passo :)