Em um teste de tração de um corpo de prova, as extremidades da amostra são forçadas recebendo uma tensão mecânica.
Durante o ensaio, a força F necessária para distender a amostra de um comprimento L é medida através de um equipamento, o equipamento fornece os seguintes resultados:
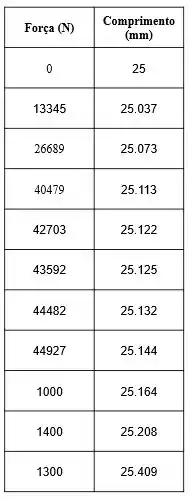
A amostra tem um raio de 6.4 mm, utilizando dessas informações plote a curva da tensão em função da deformação do material.
Dica: para isso utilize as seguintes equações para tensão e deformação respectivamente
Onde o L,A0 e F são respectivamente o comprimento, a área e a força aplicado no corpo.
Passo 1
A questão em si é um dos exemplos mais batidos para aqueles que atuam na engenharia, onde você consegue observar qual a deformação de um determinado material sob a ação de um campo de tensão.
Para isso utilizamos os dados experimentais obtidos pela máquina e utilizamos as equações que foram disponibilizadas no problema para o cálculo da tensão e da deformação do material.
Então o algoritmo se torna:
1-Implementação da entrada de dados, colocar os valores de
2-Cálculo da Área da amostra, da tensão e deformação
3-implementação do plot
4-formatação da curva.
Passo 2
Primeiro passo é a criação dos vetores de entrada no Si:
Cálculo da área, tensão e deformação no SI
Agora iremos chamar o plot da tensão em função da deformação
E finalizamos formatando os eixos do gráfico:
Passo 3
Implementando o código no matlab ele fica da seguinte forma:
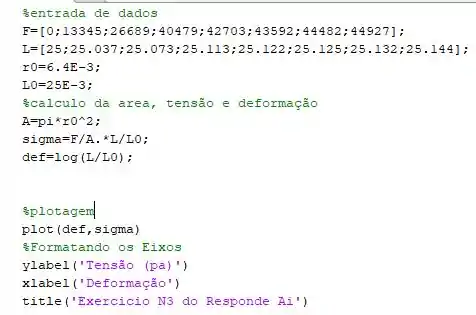
Executando o código podemos obter a seguinte curva:
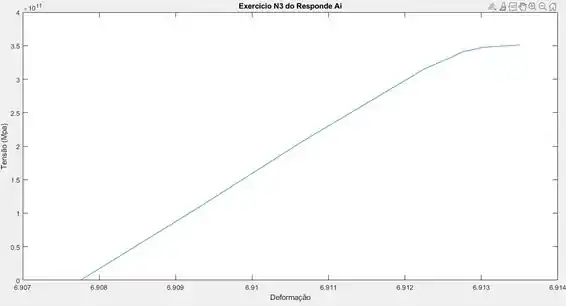
Resposta
Ei, a resposta está no passo a passo :)