O limite de escoamento é uma propriedade dos materiais que define o valor máximo de uma determinada pressão na qual o material apresenta características de uma falha.
Em geral ele é função de diversos parâmetros inclusive a taxa com que o material se deforma (alonga, enverga, comprime e etc.).
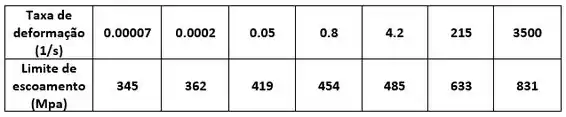
Os dados a seguir dão o limite de escoamento de um certo tipo de aço em várias taxas de deformação:
Estudiosos geraram a seguinte equação para modelar o limite de escoamento desse material:
Plote os dados experimentais e também a equação que os estudiosos descobriram e responda se a equação realmente reproduz os dados experimentais.
Obs: em vez de usar a função , use uma a função a sintaxe é idêntica a diferença é que a função plota o eixo dos todos em escala logarítmica deixando a visualização nesse caso melhor.
Passo 1
Opa galerinha aqui estamos em um problema de curva bidimensional, a ideia aqui é plotar tanto a curva quanto os pontos experimentais para ver se a equação realmente se aproxima dos dados experimentais.
Um problema de uma curva bidimensional é configurado quando queremos plotar uma curva onde nós temos uma variável dependente e uma única variável independente.
No nosso caso a variável dependente é o limite de escoamento enquanto a independente é a taxa de deformação.
Para realizar o plot de uma curva bidimensional em escala logarítmica precisamos apenas da função e para executar essa função precisamos de dois argumentos vetoriais.
O primeiro argumento é o eixo das abscissas que aqui será a taxa de deformação e o segundo argumento é o eixo das ordenadas que é o limite de escoamento.
A função ela vai imprimir os dados em um gráfico similar a função , porém irá ajustar o eixo para que possamos ter uma melhor visualização, o deixando em escala logarítmica.
Para comprar as visualizações, vamos tanto gerar o gráfico pela função , quanto pela função
Como vamos plotar tanto os dados experimentais quanto a função em um mesmo gráfico para compará-los, para o cálculo da função iremos precisar criar um vetor taxa de deformação.
Esse vetor ela irá variar de 0.000007 até 3500, como aqui temos muitos pontos iremos colocar uma variação de 1 arbitrariamente, você pode colocar qualquer valor que achar melhor.
O segundo vetor que é o limite de escoamento será criado a partir da função calculada no vetor taxa de deformação.
Uffa, Belezinha? Então vamos escrever nosso algoritmo:
1-Implementação dos dados experimentais
2-Criação do vetor taxa de deformação
3-cálculo da função limite de escoamento sigma
4-Plotagem dos gráficos e organização do mesmo.
Passo 2
Agora que criamos o algoritmo basta apenas transformá-lo em um código.
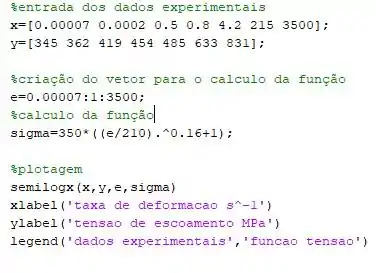
Primeiramente vamos implementar os vetores com os dados experimentais:
Vamos chamar a taxa de deformação experimental de e a tensão de escoamento experimental de .
Agora que inserimos os dados experimentais vamos calcular as funções, para isso vamos primeiro criar um vetor auxiliar taxa de deformação para o cálculo da função sigma:
Lembrando de colocar o “.” Antes da operação de potenciação pois estamos aplicando a função a cada elemento do vetor .
Agora que criamos todos os vetores, precisamos apenas criar os plot.
Primeiramente vamos criar o plot usando a função , lembrando que precisamos de dois argumentos para a função plot.
Primeiramente o eixo das abscissas e depois os eixos das ordenadas:
Agora vamos plotar também as funções nesse mesmo gráfico e para isso preciso apenas inserir novamente as variáveis dentro do mesmo plot.
Para deixar o gráfico de uma forma organizada vamos inserir algumas legendas nele junto com a nomeação dos eixos.
Primeiramente vamos nomear os eixos, utilizando as funções e, a sua sintaxe é a seguinte
Precisamos apenas escrever o texto dos eixos dentro de parênteses e aspas simples.
Assim, estamos imprimindo nos gráficos os nomes dos eixos.
Como nós temos duas curvas em um mesmo gráfico ficaria legal nomeá-las, né?
Para isso vamos utilizar a função e sua sintaxe é o seguinte:
Apenas chamar a função e colocar entre parênteses os nomes das curvas, o primeiro nome ela automaticamente vai associar aos dois primeiros argumentos da função e o segundo nome aos segundos argumentos da função
E para indicar qual é, é só inserir na ordem e separar os nomes com uma vírgula simples.
Uffa, se digitou tudo certinho finalmente o seu código deve estar mais ou menos assim:

Executando o código iremos gerar a seguinte função:

Passo 3
A exibição ficou horrível né? Sabe porquê?
A resposta é a seguinte, os primeiros pontos são bem próximos, mas se você analisar os últimos pontos são muitos distantes e isso prejudica a visualização do plot.
A escala logarítmica surge para meio que ajustar o eixo X e você analisar melhor a plotagem.
Então vamos fazer o seguinte, apaga a palavra no código e coloca e o resto permanece intacto, logo o seu código ficará assim:
E se você executar esse seu código aparecerá o seguinte plot:

Bem melhor de visualizar né?
Sabe o que fizemos? Apenas olhe o eixo do gráfico.
Isso ae, modificamos a escala do gráfico e agora conseguimos ver que o modelo se aproxima relativamente bem dos dados experimentais.
Pois nenhum modelo teórico irá se aproximar 100% dos dados experimentais.
Resposta
Ei, a resposta está no passo a passo :)