Um circuito RLC em corrente alternada pode ser modelado pela seguinte equação:
Onde e são respectivamente a indutância do indutor, resistência do resistor e a capacitância do capacitor.
Utilizando a equação acima em conjunto com os dados fornecidos abaixo, gere uma superfície tridimensional e calcule o valor de para qual o valor de seja máximo.
Dados:
Passo 1
Aqui é uma questão de simples execução, que pede para plotar a superfície tridimensional com os valores de corrente, em função da resistência do resistor e da frequência angular do sistema.
Porém, para responder essa questão precisamos de alguns detalhezinhos importantes. Primeiramente, precisamos sempre nos lembrar de criar a malha através da função meshgrid.
A malha ela surge como uma alternativa para indicar que a variável está associada com o par ordenado . Se apenas indicarmos o vetor e depois o vetor teremos apenas dois vetores cada um com uma única dimensão e eles não estão formando um plano. Então, a função meshgrid surge para corrigir isso.
Ela pega o vetor em conjunto com o vetor e unifica eles para formar um espaço de dimensão 2 que chamamos no ensino médio de plano cartesiano, ou seja, ela cria o plano para que possamos plotar a superfície 3D.
Segundamente, para encontrar a frequência angular precisamos nos lembrar da seguinte relação:
Uma vez que sabemos disso, precisamos elaborar o algoritmo para uma melhor compreensão do programa, sendo assim o algoritmo é dado por:
1-Entrada de dados
2-Criação da malha
3-Cálculo do
4-plotagem da superfície e das curvas de nível.
5-formatação do gráfico.
Passo 2
Uma vez criado o algoritmo, precisamos apenas inserir no Matlab. O código primeiramente é
composto pela entrada de dados que corresponde a:
Aqui foi adotado um incremento de 1, pois o intervalo já é demasiadamente grande.
Se colocássemos um intervalo pequeno, ficaria muitos pontos e o computador poderia demorar mais para rodar o programinha.
Agora precisamos criar a malha e como nossa função depende de , temos que eles fazem os papéis dos eixos , então a função meshgrid se torna:
Uma vez que criamos a malha precisamos calcular a função I
Agora precisamos criar a função para criação da superfície. No argumento, escrevemos primeiro as variáveis R e w, com os pares ordenados da nossa malha. Depois escrevemos a variável que contém os valores da função, que definem a altura da nossa superfície, ou seja, a variável I.
Agora precisamos apenas formatar o gráfico utilizando as funções label
Passo 3
O código em Matlab ficará algo mais ou menos assim:

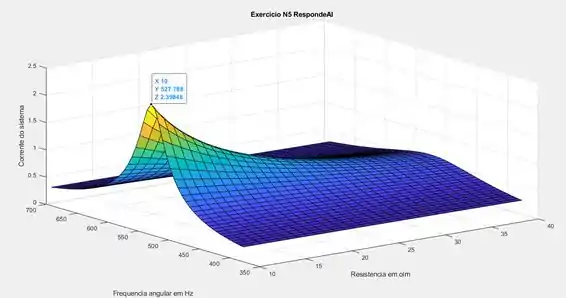
Executando o código poderemos obter a seguintes curva:
Resposta
Ao clicar no ponto mais alto da curva conseguimos obter um valor de frequência que é aproximadamente 527.78 hz, que esse corresponde a frequência de ressonância.