As moléculas de um gás confinado em um recipiente fechado movem-se aleatoriamente com velocidade que seguem a distribuição de maxwell, a distribuição de maxwell é dada pela seguinte equação:
Onde M é a massa molar do gás que corresponde a 0,032 kg/mol , , é a temperatura do gás em kelvin e v é a velocidade das partículas.
Plote a variação de em função da variação de e T, para uma variação:
Obs: os números de pontos em ambos os vetores para a criação da malha precisam ser iguais.
Passo 1
Aqui é uma questão simples onde o foco é a plotagem da superfície da equação dada na questão, a distribuição de maxwell é uma das equações mais importantes da mecânica estatística clássica pois explica diversos fenômenos observados dentro da física.
O Algoritmo da resolução do problema é dado por:
1-Entrada de dados: vetor e o vetor
2-Criação da malha
3-Cálculo do
4-plotagem da superfície
5-formatação do gráfico.
Passo 2
Uma vez criado o algoritmo precisamos apenas inserir no Matlab, o código primeiramente é
composto pela entrada de dados que corresponde a:
Como o vetor T vai ter 250 pontos, precisamos fazer com que o vetor v tenha 250 elementos logo podemos pegar o incremento e dividir 1000/250 logo
Os demais dados são:
Agora precisamos criar a malha:
Uma vez que criamos a malha precisamos calcular a função Z
Agora precisamos criar a função para criação da superfície
Agora precisamos apenas formatar o gráfico utilizando as funções label
Passo 3
O código em Matlab ficará algo mais ou menos assim:
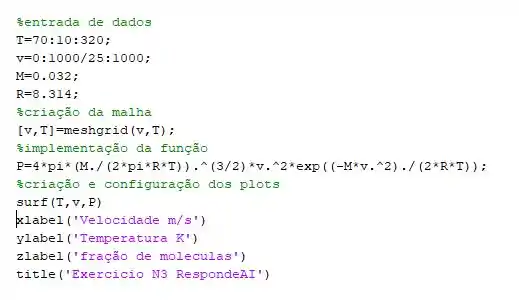
Executando o código poderemos obter a seguintes curva:

Resposta
Ei, a resposta está no passo a passo :)