A tensão em um determinado material é definida como a força por unidade de Área e é uma das entidades mais importantes para engenharia pois é a partir dela que podemos identificar se um equipamento está próximo de uma determinada falha.
Sendo assim a componente de tensão devido aos momentos de flexão e aplicados em um ponto arbitrário na seção reta de uma viga retangular é dada por:
Onde e são os momentos de inércia de cada uma das faces relevantes, definidos por:
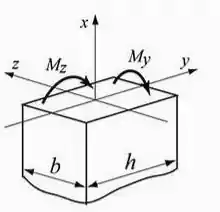
Determine e plote um gráfico da tensão normal sobre a seção reta mostrada na figura abaixo, dado que:
Passo 1
Opa galera, aqui temos um problema de uma superfície tridimensional e para verificar isso basta analisarmos a função dada.
Analisando a função temos que a função tensão depende de duas variáveis independentes que é as variáveis sendo assim o plot da função tensão tem três eixos.
A função tensão e as variáveis e como geram três eixos em um gráfico se caracterizam como um problema de uma superfície tridimensional.
Para resolver esse problema vamos utilizar a função para plotar a função, pois a função é uma das funções responsáveis para o plot de superfícies tridimensionais no Matlab.
Más antes disso temos que utilizar a função , a função tem o papel no nosso programinha de pegar dois vetores de entrada e transformá-los em um plano bidimensional para que assim possamos plotar a nossa função.
Esse plano bidimensional é extremamente importante pois nossa superfície é plotada sobre ele, esse plano recebeu o nome comumente no ensino médio de plano cartesiano.
Sendo assim o algoritmo para a resolução do nosso problema é dado por:
1-Entrada dos dados do problema.
2-Criação dos vetores
3-utilização da função meshgrid para gerar o plano.
4-Cálculo da função tensão.
5-plot do gráfico e organização do mesmo.
Passo 2
Agora que já criamos o algoritmo basta transformá-lo em nosso códigozinho do Matlab.
Primeiramente vamos implementar a entrada de dados
Agora vamos criar os vetores e , para não ficar o programa com muitos pontos vamos colocar um incremento que corresponde a seu valor máximo dividido por
Agora que criamos o vetor precisamos criar a malha com a função , cuja a sintaxe se segue colocando as variáveis de saída dentro de colchetes e as variáveis de entrada dentro de parênteses logo após chamar a função.
Uma vez que criamos a malha, precisamos apenas calcular a função. Lembrando que estamos realizando a operação a cada elemento da saída da função
Agora que criamos a função sigma vamos criar o plot.
Passo 3
Para chamar a função precisamos de 3 argumentos, o primeiro e o segundo argumento é a saída da função meshgrid que corresponde aos eixos do plano cartesiano.
E o último argumento é justamente a função que queremos plotar.
E para finalizar vamos nomear os eixos para a superfície ficar de uma forma mais organizada.
Para isso utilizando as funções e sua sintaxe é a seguinte:
vamos digitar o eixo que queremos nomear, por exemplo, se eu quero o eixo vou escrever.
Após escrever isso vou abrir os parênteses e escrever um string com o nome do eixo.
Lembrando que o string criamos escrevendo o texto em aspas simples, ou seja, deve ficar assim:
E seguindo o mesmo passo a passo nos demais eixos:
Logo seu código deve ficar algo mais ou menos assim:

Executando o código irá obter a seguinte superfície:

Resposta
Ei, a resposta está no passo a passo :)