A escada de um caminhão do corpo de Bombeiros pode ser erguida verticalmente (ângulo ), girada em relação ao eixo (ângulo ) e pode ser alongada (distância r).
Inicialmente, a escada repousa sobre o caminhão, , e .
À medida que a escada é movida para uma nova posição, os ângulos e modificam e aumentam a uma taxa de e , respectivamente e a escada se alonga a uma taxa de .
Determine e plote a posição da extremidade (ponta) da escada para 10 segundos de operação.

Passo 1
Opa pessoal, aqui temos um probleminha de curva tridimensional.
Esse probleminha se configura como uma curva tridimensional porque ele pergunta a posição da extremidade da escada no espaço, ou seja, precisamos do valor de que descrevem a posição da ponta da escada em qualquer lugar no no espaço.
Mas não é só isso, a movimentação das variáveis está amarrada com as variáveis e .
Logo precisamos arrumar alguma função que faça as variáveis variar conforme as variáveis e modificam seus valores e essas funções recebem o nome de coordenadas esféricas e são definidas pelo cálculo diferencial pelo conjunto de tais equações:
Essas equações servem basicamente para descrever o movimento de algum corpo no espaço tridimensional a partir de variáveis trigonométricas como e .
Sendo assim, vamos utilizar essas funções para descrever o movimento da escada no espaço tridimensional.
Agora para essas funções variar precisamos definir os vetores pois elas dependem dessas três quantidades, mas lembrando que os ângulos precisam estar em radianos.
E finalmente para resolver o problema vamos utilizar a função , pois queremos ver a trajetória de um único ponto e essa função ela imprime justamente as trajetórias desse ponto.
Sendo assim, o algoritmo se torna:
1-implementação dos vetores .
2-implementação das coordenadas esféricas
3-chamar a função plot3d e analisar a curva
Passo 2
Primeiramente vamos definir o vetor , para isso precisamos da informação da questão que a variação dele é de e começando do valor 0.
Porém para utilizar as funções precisamos converter isso em radianos utilizando aquela formulinha que aprendemos no ensino médio que dada por:
Logo, o incremento se torna:
e após segundos temos que:
E realizando a mesma operação para o temos
E após segundos temos:
Logo os vetores se tornam:
E por último temos o vetor com um incremento de que após segundos aumenta mais 6 metros na escada, gerando assim:
Agora que conseguimos criar o algoritmo, vamos criar o códigozinho no Matlab.
Primeiramente vamos inserir os vetores no Matlab.
Agora vamos implementar as coordenadas esféricas, mas lembre-se, tanto os ângulos quanto o raio são vetores e as operações são feitas termo a termo.
Logo precisamos colocar o “.” Para indicar que é feito termo a termo no Matlab, deixando as expressões assim:
Passo 3
E para finalizar vamos chamar o , para chamar essa função precisamos de três argumentos.
O primeiro argumento corresponde ao eixo , o segundo ao eixo e o terceiro o eixo .
Sendo assim a função fica:
Se você digitou seu código tudo certinho, temos o seguinte código:

Executando o código geramos a seguinte curva:

Passo 4
Para localizar a posição da escada no espaço basta clicar na pontinha do final da curva na sua janela gráfica e irá aparecer a seguinte informação:
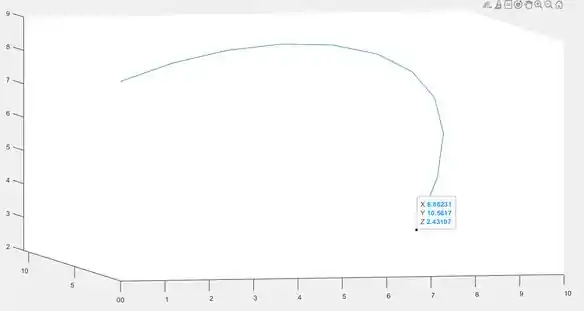
Que corresponde ao ponto:
Resposta
A posição da extremidade da escada após 10 segundos se torna: