Três lados de uma placa retangular
São mantidos à temperatura de 0 °C, e o outro lado é mantido à temperatura de 80 °C como mostrado na figura abaixo:

Determine e plote a distribuição de temperatura da placa sabendo que a função que gera essa curva é dada por:
Passo 1
Opa galerinha iae tudo bem?
Quando estudamos em engenharia problemas de transferência de energia entre corpos geralmente as funções que descrevem como a temperatura varia no espaço são dadas por funções dessa natureza.
Esse tipo de função recebe o nome de séries, ou seja, ela é uma soma de um bocado de termos.
Por exemplo quando n for igual a 1 temos:
Já quando n for igual a 2 temos:
Sendo assim, quanto mais termos nos damos a n, mais somas de senos a função detém e consequentemente a função descreve melhor a física do problema.
Porém, aqui já conseguimos notar que existe uma dificuldade monstruosa de fazer isso manual, certo? Imagine você colocar n=50… isso fica bem inviável de se fazer manualmente.
Então é aí que surge o Matlab, o estudo dessas funções auxiliada com as ferramentas do Matlab é o que utilizamos para o estudo para descrever como uma determinada temperatura varia ao longo de uma placa metálica.
Como a variável temperatura que é nossa variável dependente varia com duas variáveis independentes que é os pontos aqui temos um problema de uma superfície tridimensional.
Para a resolução de um problema de uma superfície tridimensional usamos a função mas para criar a função surf, precisamos criar o plano cartesiano.
O plano cartesiano é criado utilizando a função meshgrid, cujo o foco é pegar os dois vetores das variáveis independentes e unificá-los em uma malha, gerando o plano cartesiano.
Onde faz com que os vetores se torne uma matriz para que nós possamos assim utilizar a função e plotar a superfície sobre o plano.
Ahh aqui como mostramos no início temos uma soma de funções que depende de um certo índice n e para isso vamos utilizar as estruturas de repetição para ficar realizando essas somas de forma automática.
Além disso, a nossa função tem termos que depende de e outros que depende de , então vamos precisar montar duas somas, a primeira vai calcular todas as parcelas que depende de e a outra todas que dependem de , beleza?
Sendo assim o nosso algoritmo se torna:
1-Entrada de dados – Aqui vamos inserir os dados do problema
2-Criação dos vetores e
3-Criação do plano cartesiano com a função
4-início do primeiro laço para o cálculo das parcelas de
4.1- Segundo laço para o cálculo das parcelas de
4.2-inserir a função
4.3-finalizar os laços
5-plotar com a função e organizar o gráfico.
Passo 2
Agora que criamos o algoritmo vamos montar o nosso programinha, primeiramente vamos colocar a entrada de dados:
Agora precisamos indicar o número n, pois é ele que vai dizer quantas vezes vamos somar uma função seno na nossa função temperatura, belezinha?
Vou colocar um número pequeno pois se colocar muito grande o cálculo fica pesado, então arbitrariamente vou colocar:
Agora vamos criar os vetores para não ficar com um grande número de pontos vamos colocar as variações em torno do seu valor máximo dividindo por 20, sendo assim:
Agora que criamos os vetores vamos criar o plano cartesiano com a função onde a sintaxe é a seguinte:
Primeiramente a variável de saída deve estar entre colchetes e a variável de entrada precisa estar entre parênteses, portanto:
Agora vamos a parte complicada, o primeiro laço ele vai fazer com que a função varie e calcule seu valor em todos os valores de arbitrariamente vamos dar os valores de i para ele e fazemos ele variar até o número de elementos da matriz com a função.
Essa é uma função já vista antes que nos fala o número de elementos dentro de um vetor, ou seja, ela o número de vezes que o for vai se repetir é igual ao número de elementos dentro do vetor x.

O segundo laço faz com que a função varie em todos os valores de e vamos dar um nome arbitrário de para ele e fazemos ele variar até o número de elementos da matriz com a função
Lembrando que quando a=0, analisando a figura do problema a temperatura é 0, logo o , fazendo com que o laço comece de

E agora precisamos inserir as somas correspondentes a todos n termos do polinômio com a função.
Lembrando que estamos calculando cada elemento da função em cada elemento da matriz, logo o produto do seno pelo seno hiperbólico precisa colocar um “.” Para indicar que a operação é termo a termo.
Após finalizar o laço do temos que toda a matriz é multiplicada pelo termo
Logo essa última parte fica:

Sendo assim, a estrutura de repetição completa fica:

E para finalizar vamos chamar a função e para isso vamos precisar de 3 argumentos.
Os dois primeiros argumentos é a saída da função obrigatoriamente, sendo assim, a função fica:
E para finalizar o último argumento é a variável que queremos plotar que no caso é a temperatura, logo:
E agora vamos nomear os eixos utilizando as funções para organizar melhor a janela gráfica.
Para isso vamos digitar o eixo que queremos nomear por exemplo se eu quero o eixo vou escrever:
Após escrever isso vou abrir o parênteses e escrever um string com o nome do eixo.
Lembrando que o string criamos escrevendo o texto em aspas simples, ou seja, deve ficar assim:
E seguindo o mesmo passo a passo nos demais eixos:
E finalmente seu código deve ficar algo mais ou menos assim:
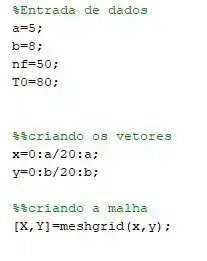

Passo 3
E finalmente se executar o código temos a seguinte superfície.

Resposta
Ei, a resposta está no passo a passo :)