Construa a superfície de revolução dada pela equação abaixo:
Sob o domínio e
Passo 1
Aqui é uma questão simples onde o foco é a plotagem da superfície de revolução da equação dada na questão.
Para a resolução da questão precisamos utilizar a função meshgrid, pois para a criação de superfícies 3D precisamos criar um artifício matemático que chamamos de malha.
Quando estamos plotando curvas em uma única dimensão, nós sempre temos uma função que está associada à variável . Aqui, em 2 dimensões, temos uma função associada às variáveis e .
E a malha surge como uma alternativa para indicar que a variável está associada com o par ordenado .
Porém se indicarmos o vetor e depois o vetor teremos apenas dois vetores cada um com uma única dimensão e eles não estão formando um plano.
Então, a função meshgrid surge para corrigir isso.
Ela pega o vetor em conjunto com o vetor e unifica eles para formar um espaço de dimensão 2 que chamamos no ensino médio de plano cartesiano, ou seja, ela cria o plano para que possamos plotar a superfície 3D.
Conhecendo essas informações, temos que o algoritmo da resolução do problema é dado por:
1-Entrada de dados: vetor x e o vetor y
2-Criação da malha com a função meshgrid
3-Cálculo do Z
4-plotagem da superfície
5-formatação do gráfico.
Passo 2
Uma vez criado o algoritmo, precisamos apenas inserir no Matlab. O código primeiramente é
composto pela entrada de dados que corresponde a:
Aqui utilizamos um incremento de 0.01 pois queremos que a distância entre os dois pontos sucessivos seja pequena, pra melhorar a precisão da nossa superfície.
Como já foi comentado o Matlab não gera uma curva contínua propriamente dita, ele simplesmente calcula os valores da função em diversos pontos. Porém, esses pontos são tão próximos um do outro que quando imprimimos em um gráfico temos a impressão que a curva é contínua.
Agora precisamos criar essa malha de pontinhos no plano xy :
Uma vez que criamos a malha precisamos calcular a função Z
Agora precisamos criar a função para criação da superfície e pra isso vamos usar o comando . Lembrando da sua sintaxe, primeiramente se coloca as variáveis independentes, que são as variáveis de saída da função meshgrid (x e y), e por último a variável que contém os valores da nossa função (z):
Agora precisamos apenas formatar o gráfico utilizando as funções label
Passo 3
Executando o código podemos obter a seguinte curva:
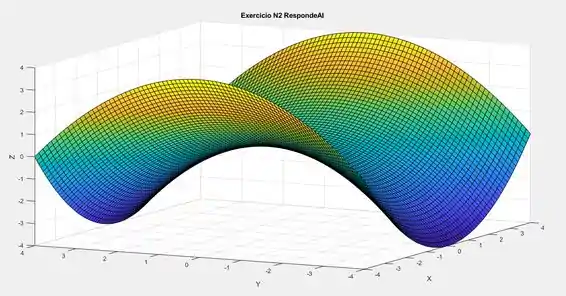
Resposta
Ei, a resposta está no passo a passo :)