A figura abaixo ilustra um cilindro condutor maciço de raio que é percorrido por uma corrente elétrica , onde é a distância radial até o eixo de simetria do cilindro.
- Calcule a expressão para a corrente elétrica quando a densidade de corrente , onde é uma constante.
- Calcule a expressão para a corrente elétrica quando a densidade de corrente , onde é uma constante.
- Dentre as correntes calculadas nos itens (a) e (b), qual é a maior? Justifique sucintamente o fato de uma corrente ser maior que a outra.
Passo 1
a) Para resolvermos os dois primeiros itens, vamos dar uma olhada para a figura abaixo, que mostra apenas a seção transversal atravessada pela corrente , que é perpendicular à página e está saindo dela, na direção e sentido de .
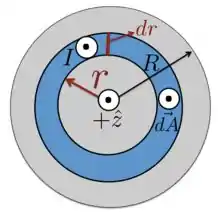
Neste caso, podemos escrever o vetor área como
cujo módulo obtivemos considerando o elemento de área mostra na figura acima. Essa é a área atravessa pela corrente , cujo vetor densidade de corrente é . Portanto, e são paralelos e vamos usar isso também para matar o item b depois.
Como é uma densidade superficial de corrente, ou seja, é uma grandeza que dá a quantidade de corrente por unidade de área, a corrente é escrita como:
que é a integral do produto escalar entre e . Nesse caso, como e são paralelos, fica
Passo 2
b) Aqui, vamos substituir a outra expressão para :
que simplificada tem esta outra “cara”:
Passo 3
c) A corrente do item a) é maior do que a do item b): . Isso acontece porque a densidade de corrente no item a) aumenta linearmente com a distância a partir do centro, ou seja, à medida que área atravessada pela corrente aumenta, a quantidade de corrente que atravessa essa área também aumenta resultando em uma corrente total maior.
Já no caso do item b), a densidade de corrente diminui linearmente com , o que significa que à medida que área pela qual a corrente passa aumenta, a quantidade de corrente diminui, o que dá, no final das contas, uma corrente total menor.
Resposta
- , pois a densidade de corrente no item a) aumenta com e a do item b) diminui com à medida que a área aumenta.