Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Diagrama de Blocos

Ver Teoria
Exercício 31245678

Enunciado

Dadas as EDO’s abaixo, encontre as expressões para Y 1 ( s ) e Y 2 ( s ) e representa as variáveis através de um diagrama de blocos.

2 d 2 y 1 t d t 2 + 3 d y 1 t d t + y 1 t = x 1 t + x 2 ( t )

5 d y 2 t d t + y 2 t = 2 x 2 t + y 1 ( t )

Passo 1

Nessa questão nós precisamos fazer duas coisas, primeiro encontrar as funções de Y 1 ( s ) e Y 2 ( s ) e em seguida representar essas funções em um diagrama de blocos.

O primeiro passo quando temos uma EDO e precisamos de uma função de transferência é aplicar Laplace.

Vamos fazer isso primeiro na primeira EDO. Para facilitar, vamos fazer isso termo a termo:

L 2 d 2 y 1 t d t 2 = 2 s 2 Y 1 ( s )

L 3 d y 1 t d t = 3 s Y 1 ( s )

L y 1 ( t ) = Y 1 ( s )

L x 1 ( t ) = X 1 ( s )

L x 2 ( t ) = X 2 ( s )

Caso você ainda tenh dúvidas sobre transformadas de Laplace, seria legal dar uma revisada nesse conteúdo aqui no Responde Aí!

Juntando tudo:

2 s 2 Y 1 s + 3 s Y 1 s + Y 1 s = X 1 s + X 2 ( s )

Colocando Y 1 ( s ) em evidência do lado esquerdo:

2 s 2 + 3 s + 1 Y 1 s = X 1 s + X 2 ( s )

Por fim, isolando Y 1 ( s ) :

Y 1 s = 1 2 s 2 + 3 s + 1 X 1 s + 1 2 s 2 + 3 s + 1 X 2 ( s )

Passo 2

Vamos fazer o mesmo para a segunda EDO agora.

Aplicando Laplace em cada termo:

L 5 d y 2 t d t = 5 s Y 2 ( s )

L y 2 ( t ) = Y 2 ( s )

L 2 x 2 ( t ) = 2 X 2 ( s )

L y 1 ( t ) = Y 1 ( s )

Juntando tudo:

5 s Y 2 s + Y 2 s = 2 X 2 s + Y 1 ( s )

5 s + 1 Y 2 s = 2 X 2 s + Y 1 ( s )

Y 2 s = 2 5 s + 1 X 2 s + 1 5 s + 1 Y 1 ( s )

Passo 3

Agor já temos as expressões de Y 1 ( s ) e Y 2 ( s ) :

Y 1 s = 1 2 s 2 + 3 s + 1 X 1 s + 1 2 s 2 + 3 s + 1 X 2 ( s )

Y 2 s = 2 5 s + 1 X 2 s + 1 5 s + 1 Y 1 s

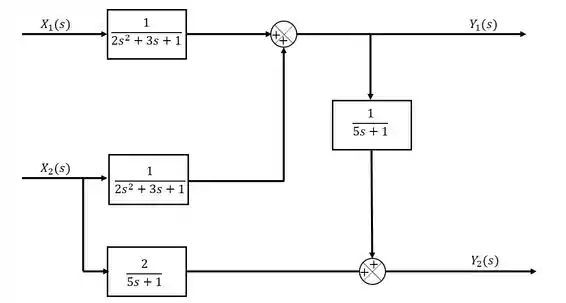
A partir delas, devemos esboçar o diagrama de blocos do sistemas. Perceba que esse sistema possui duas saídas, Y 1 ( s ) e Y 2 ( s ) e duas entradas, X 1 ( s ) e X 2 ( s ) . Sendo assim, vamos começar representando as duas saídas e as duas entradas:

Vamos ir montando o nosso diagrama por partes então.

Para começar, vamos olhar para a equação de Y 1 ( s ) . Essa variável é a soma da entrada X 1 ( s ) multiplicada por uma função com a variável X 2 ( s ) multiplicada por uma função. Representando isso no diagrama, teremos:

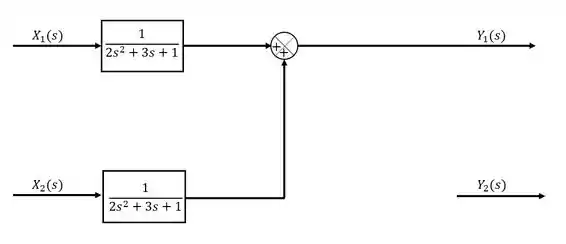
Passo 4

Agora, temos que fazer o mesmo para a variável Y 2 ( s ) .

A variável Y 2 ( s ) também depende de X 2 ( s ) , entretanto, a função que multiplica essa entrada é diferente, o que indica que teremos que adicionar um novo bloco. Além disso, ela também depende da outra saída, Y 1 ( s ) . Sendo assim, o diagrama de blocos ficará:

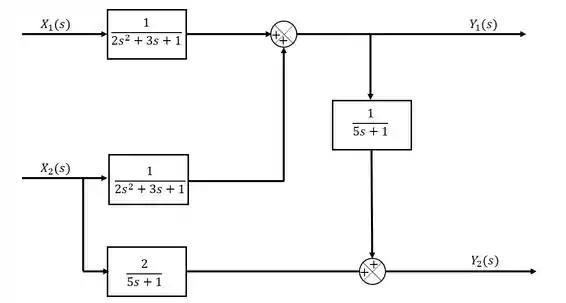
Obs: pode existir mais de uma maeira de fazer a representação em diagrama de blocos, essa é apenas uma delas.

Resposta

Exercícios de Livros Relacionados

Uma comporta retangular (de largura w = 2 m) é articulada conforme mostrado, com um batente na borda inferior. Em que profundidade H a comporta estará prestes a abrir?
Considere uma caneca de chá (com 65 mm de diâmetro). Imagine a caneca cortada simetricamente ao meio por um plano vertical. Encontre a força que cada metade experimenta devido a coluna de 80 mm de chá
Uma janela de acesso, na forma de um triângulo isósceles e articulada no topo, é colocada na parede vertical de uma forma contendo concreto líquido. Determine a força mínima que deve ser aplicada no p
Uma comporta plana, de espessura uniforme, suporta uma coluna de água conforme mostrado. Determine o peso mínimo da comporta necessário para mantêla fechada.
A comporta parabólica mostrada na figura tem 2 metros de largura e é articulada em O ; c = 0,25m - 1 , D = 2m e H = 3m . Determine (a) o módulo e a linha de ação da força vertical sobre a comporta cau