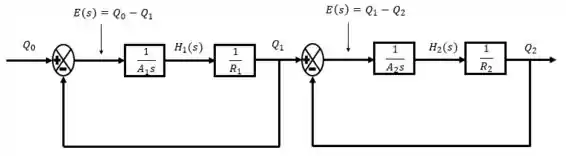
Considere o sistema constituído por dois tanques em cascata conforme mostrado na figura abaixo.
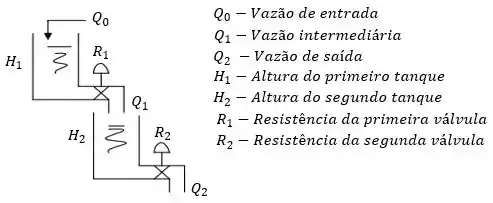
Sendo as equações que governam esse sistema no domínio da frequência:
Obter o diagrama de blocos que relaciona a saída com a entrada
Passo 1
Nessas questões em que temos as equações que governam o sistema e nos é pedido para obter o diagrama de blocos, trabalhamos como se estivéssemos montando um quebra cabeça.
Nós temos dois componentes do diagrama de blocos para nos auxiliar: o somador e o ponto de ramificação.
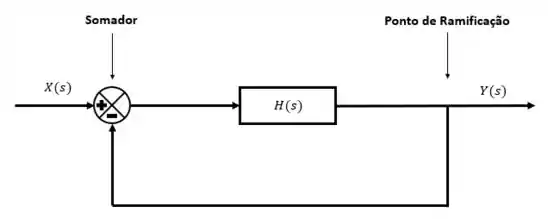
Muitas vezes é necessário rearrumar a equação de governo para facilitar a construção do diagrama de blocos. No nosso caso, será necessário isolar as alturas e .
Passo 2
Como temos duas equações de governo com uma diferença entre termos de vazão, vamos expressar isso como um somador.
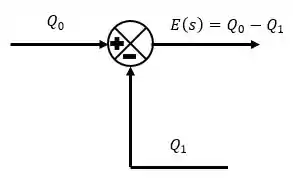
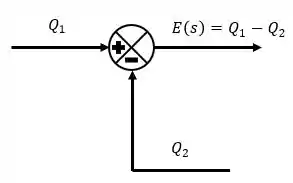
Passo 3
Após utilizarmos os somadores, verificamos que nossos erros são bem parecidos com as equações de governo. Precisamos agora rearrumarmos as equações para verificarmos o que precisa ser multiplicado ao erro para fazer aparecer as variáveis e .
Rearrumando elas,
Ou seja, aos nossos erros:
Multiplicamos:
Isso vai ser representado no diagrama de blocos como uma função de transferência em que entra os erros e sai as alturas .
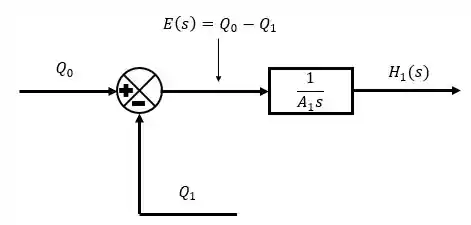
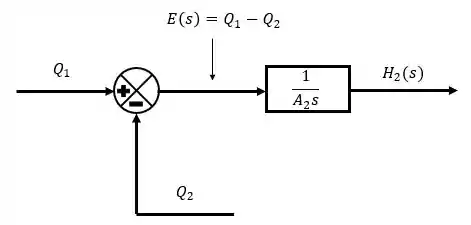
Passo 4
Estamos próximo do fim, nosso próximo recurso a ser utilizado é um ponto de ramificação, pois vemos que tanto no primeiro quanto no segundo diagrama de blocos, temos que fazer aparecer as vazões e .
Nós já usamos as duas primeiras equações de governo, temos mais duas para poder ser utilizadas.
Rearrumando as duas para deixar em evidência as vazões e verificarmos o que está faltando.
Opa, verificamos que temos uma função de transferência aí também, que relaciona minhas alturas como entrada e me devolve como saída as vazões. Aplicando isso no diagrama de blocos.
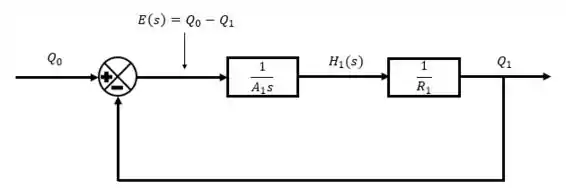
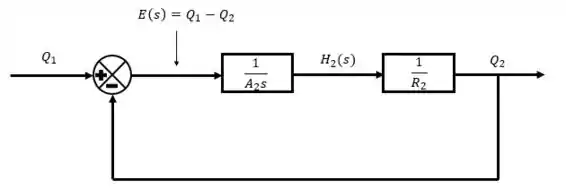
Como precisamos correlacionar com , unimos os diagramas de blocos.
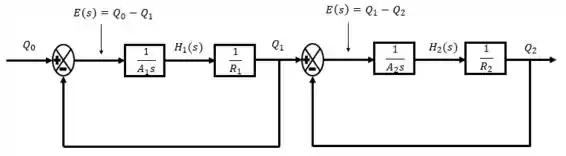
Resposta