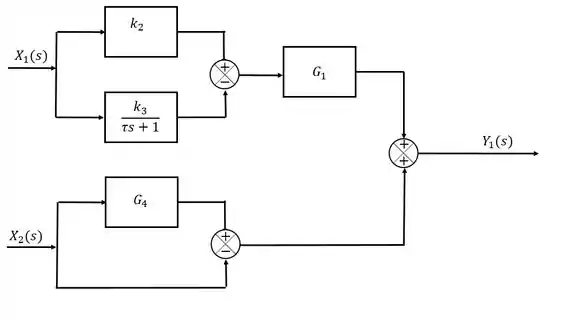
Desenhe o diagrama de blocos que representa a função de transferência abaixo:
Passo 1
Para montar esse coleguinha, precisamos identificar as variáveis de entrada e saída da função de transferência. Essa FT tem uma variável de saída, , e duas variáveis de entrada, e . Vamos respresentar as setas dessas variáveis então:

Passo 2
Vamos analisar o “caminho” que cada variável de entrada faz para resultar na variável de saída. A variável , multiplica uma diferença de duas funções , isso indica um ponto de ramificação em :
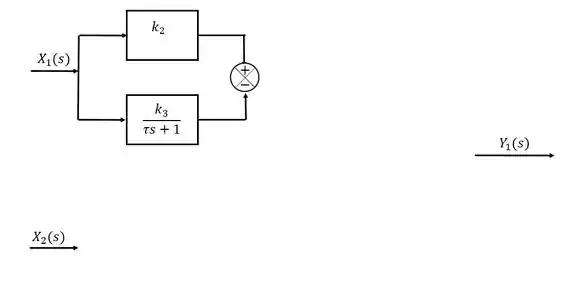
Passo 3
Ainda em é possível notar que o sinal também multiplica uma função , sendo assim:
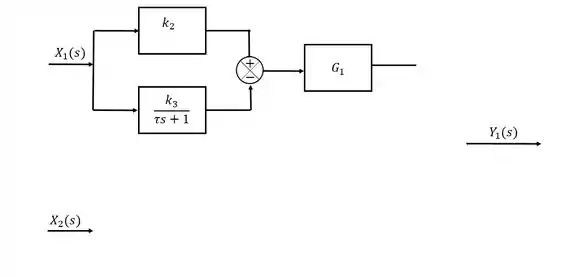
Passo 4
Em , também é possível notar um ponto de ramificação devido ao termo , portanto:
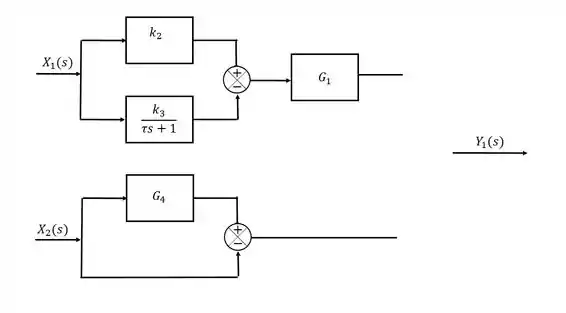
A linha reta indica que não existe nenhuma alteração no sinal, ou, em outras palavras, que a função de transferência naquele trecho é .
Passo 5
Por fim, os dois termos provenientes dos sinais de entrada se encontram e se somam, resultando nessa belezinha de diagrama aqui:
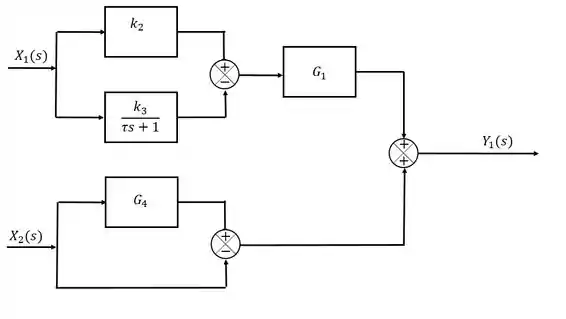
Resposta