Seja
Plote o diagrama de Bode e encontre as margens de fase e de ganho de .
Passo 1
O exercício pede para plotarmos o diagrama de Bode de e para encontrarmos a margem de ganho e a margem de fase de . Obteremos a solução do exercício com um único comando do MATLAB: .
No nosso programa, precisamos entrar com usando a função . Contudo, antes de aplicar , precisamos multiplicar os termos do numerador e do denominador de , para obtermos os polinômios cujos coeficientes servirão de entrada para .
Tendo entrado com , ela servirá de entrada para a função , que plota o diagrama de Bode já informando as margens de fase e de ganho.
Passo 2
Vamos multiplicar os termos do numerador e do denominador no próprio MATLAB mesmo, começando pelo numerador. Em um novo script, digite as seguintes linhas de código:

Na primeira linha, é definida uma variável simbólica .
Na segunda linha, criamos uma variável que armazena o numerador de no formato atual.
Na terceira linha, usamos o comando para multiplicar os termos de e gerarmos o polinômio do numerador, que é armazenado em .
Execute o programa e imprima no Command Window :

Logo, o polinômio do numerador de é .
Faça a mesma coisa para o denominador de , digitando no mesmo script as linhas de código:
![]()
Primeiramente, criamos a variável para armazenar o denominador de no formato que ele está no enunciado. Em seguida, usamos nele para gerar o polinômio do denominador, que é armazenado em . O polinômio do denominador será:
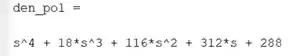
Logo, .
Passo 3
Tendo os polinômios do numerador e do denominador de , podemos usar a função para criar . Lembrando que tem a sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Em um novo script ou no mesmo onde você obteve os polinômios, crie dois vetores contendo os coeficientes dos polinômios, para servirem de entrada para . O primeiro vetor se chamará e terá os coeficientes do numerador de . Já o segundo vetor se chamará e conterá os coeficientes do denominador de .
O polinômio do numerador é e o do denominador, , logo, e ficarão assim:

Já podemos pôr logo abaixo o comando , para criar a variável , que contém .
Vamos rodar o programa digitado até agora para conferir se está tudo certo com , imprimindo no Command Window:

Está tudo certo, já podemos plotar o diagrama de Bode a partir de .
Passo 4
Plotaremos o diagrama de Bode de com o comando , que além de nos dar diagrama, ainda informa pra gente as margens de ganho e de fase. O comando tem a como sintaxe:
Ele tem como entrada uma função de transferência criada usando o comando (representada por ) e ele gera, ao executarmos o programa, um gráfico com o diagrama de Bode de , informando no título do gráfico as margens de ganho e de fase.
Para chegarmos na solução do exercício, adicione ao seu código o comando:
![]()
Execute o programa para obter a solução do exercício:
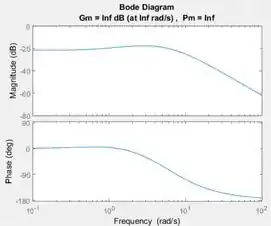
No título do gráfico, a margem de ganho é indicada por e a margem de fase, por . Temos que ambas as margens são infinitas. Mas por quê?
Note no diagrama de que a curva de a razão de amplitude está inteira abaixo de , isto é, não importa a frequência, a razão de amplitude sempre será menor do que . Isso indica que o sistema é sempre estável, isto é, podemos multiplicar o ganho por qualquer valor que o sistema permanecerá estável. Por isso a margem de ganho é infinita.
Uma margem de fase infinita indica que a malha suporta qualquer valor de atraso, pois ela permanecerá estável.
Resposta

Margem de ganho:
Margem de fase: