Usando o MATLAB, obtenha a margem de ganho, margem de fase, a frequência de e a frequência de para um sistema com realimentação unitária e função de transferência em malha aberta:

Vamos entrar com no MATLAB. Para isto, usaremos a função , que cria funções de transferência e tem a seguinte sintaxe:

A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .

Para , o polinômio do numerador é . Já o polinômio do denominador é .

Em um novo script, vamos criar duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .

A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:

Logo abaixo, já digitamos o comando , para criar e armazená-la na variável . Se quiser, você pode rodar o programa que você tem até agora para conferir se você entrou certo com . Para isto, imprima no Command Window:

Se estiver igualzinho a , pode prosseguir :)

Após entrar com , usamos o comando , que plota o diagrama de Bode de já com as margens de ganho e de fase destacadas. A função tem a seguinte sintaxe:

Ela tem como entrada uma função de transferência criada usando o comando (representada por ) e ela gera, ao executarmos o programa, um gráfico com o diagrama de Bode de , informando já no título do gráfico as margens de ganho e de fase e a frequência na qual elas foram calculadas.

Para chegarmos no resultado do exercício, adicione ao seu código o comando:

Com este comando, geraremos o diagrama de Bode de e obteremos as margens de fase e de ganho. Rodando o programa para ver o resultado, temos:

No título do gráfico, a margem de ganho é indicada por e margem de fase, por . Temos que a margem de ganho é e a margem de fase, .

Com isso, já temos as margens de ganho e de fase pedidas pelo enunciado. Mas e as frequências de e ?

Para encontrarmos as frequências, vamos relembrar como se calculam as margens de ganho e de fase usando o diagrama de Bode.

Em um diagrama de Bode, a margem de ganho é calculada encontrando a frequência onde o ângulo de fase é e fazendo a diferença entre e a razão de amplitude (no caso do gráfico gerado pelo MATLAB, ) nessa mesma frequência. Em outras palavras, isso quer dizer que a frequência onde a margem de ganho é calculada é a frequência de .

Repare que o título do gráfico diz: , informando que a margem de ganho de foi calculada em . Isso quer dizer a frequência de é .

Outra alternativa para encontrar a frequência de é clicar no gráfico de baixo, o de , e arrastar o quadradinho preto até encontrar o dado igual a , como na imagem abaixo:

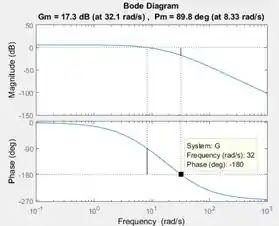
Veja que a frequência desse ponto é igual a , praticamente igual ao valor dado pelo título do gráfico. Repare também que o ponto onde é igual a está exatamente sobre a linha vertical pontilhada que indica a posição da margem de ganho no diagrama de Bode. Isso porque a margem de ganho foi determinada como eu disse acima.

Para encontrar a frequência de , vamos relembrar como se calcula a margem de fase usando o diagrama de Bode. Ela é calculada encontrando a frequência onde a razão de amplitude (no diagrama gerado pelo MATLAB, ) é e fazendo a diferença entre o ângulo de fase nessa frequência e .

Em outras palavras, isso quer dizer que a frequência onde a margem de fase é calculada é a frequência de .

Repare que o título do gráfico diz: , informando que a margem de fase de foi calculada em . Isso quer dizer a frequência de é .

Outra alternativa para encontrar a frequência de é clicar no gráfico de cima, o de , e arrastar o quadradinho preto até encontrar o dado o mais próximo possível de , como na imagem abaixo (é difícil achar exatamente o ):

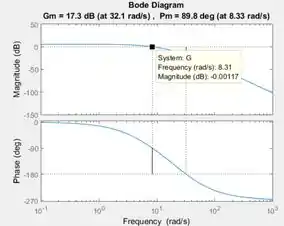
Veja que a frequência desse ponto é igual a , dando uma razão de amplitude de , bem próxima de . Repare que a frequência é bem próxima da dada no título do gráfico para a margem de fase.

Como é difícil acertar o ponto de , recomendo pegar os valores dados pelo título do gráfico.