Usando o MATLAB, determine se o seguinte processo pode ser tornado instável aumentando-se o ganho dele. Utilize argumentos baseados em resposta em frequência e critério de Bode.
Passo 1
Quando o exercício pede para determinarmos se pode se tornar instável aumentando o ganho, na real ele está nos pedindo para ver se já é estável, com outras palavras. Se ele for estável na forma que foi apresentado no enunciado, avaliando-o pelo critério de Bode, significa que tem espaço para aumentar o ganho até que o processo se torne instável.
Logo, o exercício pede para vermos se é estável ou não, nos baseando em resposta em frequência e critério de Bode. Para isto, plotaremos o diagrama de Bode de usando o MATLAB.
No nosso programa, devemos primeiro entrar com no MATLAB usando a função . Em seguida, usaremos a função para plotar o diagrama de Bode. Avaliaremos a estabilidade de usando o gráfico gerado por nosso programa, a partir do critério de Bode.
Passo 2
O primeiro passo para resolver o exercício é entrar com no MATLAB. Para isto, usaremos a função , que cria funções de transferência e tem a seguinte sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script, vamos criar duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:
![]()
Em seguida, adicione o comando abaixo para criar :
![]()
A função de transferência é armazenada na variável . Você pode ver como ficou ao rodar o programa e pedir ao MATLAB para imprimir no Command Window:

Passo 3
Tendo entrado com no MATLAB, podemos plotar seu diagrama de Bode, usando o comando , que tem a sintaxe:
Ele tem como entrada uma função de transferência (representada pela variável ), criada usando o comando do MATLAB, e ele gera um gráfico com o diagrama de Bode para .
No script criado no passo 2, adicione as seguintes linhas de código:
![]()
Além do comando para plotar o diagrama de Bode de , incluímos o comando , para que o diagrama tenha linhas de grade. As linhas de grade vão ajudar a avaliar a estabilidade de pelo critério de Bode.
Vamos rodar o programa para vermos o diagrama de Bode de :
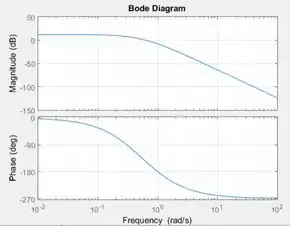
Passo 4
Com o diagrama de Bode em mãos, podemos usar o critério de Bode para ver se é estável ou não. O critério de Bode diz que um sistema é estável se a razão de amplitude for menor que na frequência em que o ângulo de fase atinge .
Lembrando que no diagrama de Bode gerado pelo MATLAB, a razão de amplitude é chamada de .
O primeiro passo, então, é achar a frequência em que o ângulo de fase é . Para isto, clique sobre a curva do gráfico de baixo, cujo eixo vertical é . Aparecerá um quadradinho preto que informa a frequência e o ângulo de fase do ponto sobre o qual você clicou.
Arraste o quadradinho até que seja igual a . Use as linhas de grade para te orientar. Ao fazer isso, você terá algo parecido com a imagem abaixo:
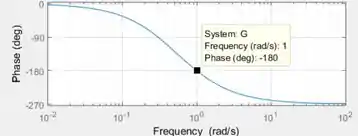
Vemos que a frequência em que o ângulo de fase é é de .
Passo 5
Sabendo que o ângulo de fase atinge em uma frequência de , vamos procurar no gráfico de cima do diagrama de Bode gerado pelo MATLAB, isto é, no gráfico cujo eixo vertical é , qual é a razão de amplitude em .
Para isto, clique sobre a curva do gráfico , para aparecer aquele quadradinho preto com as informações sobre o ponto onde você clicou. Dessa vez, ele informará a frequência e a razão de amplitude do ponto.
Arraste o quadradinho preto até atingir uma frequência de , usando as linhas de grade para se guiar. Ao fazer isso, seu gráfico de ficará com essa cara:
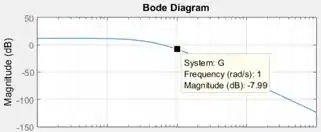
Vemos que a razão de amplitude em é , menor que . Logo, é estável.
Em outras palavras, podemos aumentar o ganho de até que o sistema se torne instável, pois podemos aumentar o ganho até que a razão de amplitude se torne maior que , partindo de no estado atual, onde a razão de amplitude é de na frequência em que o ângulo de fase é , atendendo ao critério de Bode.
Em outras palavras, temos uma “folga” de .
Resposta
É possível que o processo se torne instável aumentando-se o ganho, pois podemos aumentar o ganho até que a razão de amplitude se torne maior que na frequência em que o ângulo de fase atinge , visto que apresenta razão de amplitude negativa nessa frequência.